
【题目】已知直线![]() 与曲线
与曲线![]() 和
和![]() 分别交于
分别交于![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() ,则
,则![]() 面积的最小值为( )
面积的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
求出S△ABC![]() 2|BC|=et+t2﹣t+2,令f(t)=et+t2﹣t+2,t∈R,求出函数的导数,根据函数的单调性求出三角形面积的最小值即可.
2|BC|=et+t2﹣t+2,令f(t)=et+t2﹣t+2,t∈R,求出函数的导数,根据函数的单调性求出三角形面积的最小值即可.
由已知得B(t,et),C(t,﹣t2+t﹣2),
则|BC|=et+t2﹣t+2,
故S△ABC![]() 2|BC|=et+t2﹣t+2,
2|BC|=et+t2﹣t+2,
令f(t)=et+t2﹣t+2,t∈R,
f′(t)=et+2t﹣1,
f′(t)在R递增,又f′(0)=0,
故t>0时,f′(t)>0,t<0时,f′(t)<0,
故f(t)在(﹣∞,0)递减,在区间(0,+∞)递增,
故f(t)min=e0+0﹣0+2=3,
故S△ABC的最小值是3,
故选:C.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,现从高一学生中抽取100人做调查,得到![]() 列联表:
列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 100 |
且已知在100个人中随机抽取1人,抽到喜欢游泳的学生的概率为![]() .
.
(1)请完成上面的列联表;
(2)根据列联表的数据,是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由.
参考公式与临界值表:![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为 (为参数),直线l与曲线C交于M、N两点。
(为参数),直线l与曲线C交于M、N两点。
(1)写出直线l的普通方程和曲线C的直角坐标方程:
(2)若![]() 成等比数列,求a的值。
成等比数列,求a的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地需要修建一条大型输油管道通过720千米宽的荒漠地带,该段输油管道两端的输油站已建好,余下工程只需要在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的工程费用为108万元,铺设距离为![]() 千米的相邻两增压站之间的输油管道费用为
千米的相邻两增压站之间的输油管道费用为![]() 万元.设余下工程的总费用为
万元.设余下工程的总费用为![]() 万元.
万元.
(1)试将![]() 表示成关于
表示成关于![]() 的函数;
的函数;
(2)需要修建多少个增压站才能使总费用![]() 最小?
最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了增加某种产品的生产能力,提出甲、乙两个方案。甲方案是废除原有生产线并引进一条新生产线,需一次性投资1000万元,年生产能力为300吨;乙方案是改造原有生产线,需一次性投资700万元,年生产能力为200吨;根据市场调查与预测,该产品的年销售量的频率分布直方图如图所示,无论是引进新生产线还是改造原有生产线,设备的使用年限均为6年,该产品的销售利润为1.5万元/吨。
(Ⅰ)根据年销售量的频率分布直方图,估算年销量的平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)将年销售量落入各组的频率视为概率,各组的年销售量用该组区间的中点值作年销量的估计值,并假设每年的销售量相互独立。
(i)根据频率分布直方图估计年销售利润不低于270万的概率;
(ii)以企业6年的净利润的期望值作为决策的依据,试判断该企业应选择哪个方案。(6年的净利润=6年销售利润-投资费用)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一场小型晚会有![]() 个唱歌节目和
个唱歌节目和![]() 个相声节目,要求排出一个节目单.
个相声节目,要求排出一个节目单.
(1)![]() 个相声节目要排在一起,有多少种排法?
个相声节目要排在一起,有多少种排法?
(2)![]() 个相声节目彼此要隔开,有多少种排法?
个相声节目彼此要隔开,有多少种排法?
(3)第一个节目和最后一个节目都是唱歌节目,有多少种排法?
(4)前![]() 个节目中要有相声节目,有多少种排法?
个节目中要有相声节目,有多少种排法?
(要求:每小题都要有过程,且计算结果都用数字表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
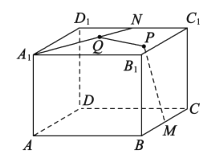
【题目】已知长方体![]() 中,底面ABCD的长AB=4,宽BC=4,高
中,底面ABCD的长AB=4,宽BC=4,高![]() =3,点M,N分别是BC,
=3,点M,N分别是BC,![]() 的中点,点P在上底面
的中点,点P在上底面![]() 中,点Q在
中,点Q在![]() 上,若
上,若![]() ,则PQ长度的最小值是
,则PQ长度的最小值是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com