
【题目】已知向量![]() ,求:
,求:
(1)![]() ;(2)
;(2) ![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:由两向量的坐标,以及两向量垂直时数量积为![]() ,列出关系式,利用同角三角函数间的基本关系化简后,求出
,列出关系式,利用同角三角函数间的基本关系化简后,求出![]() 的值,由
的值,由![]() 的范围,再利用同角三角函数间的基本关系求出
的范围,再利用同角三角函数间的基本关系求出![]() 的值. (1)由两向量的坐标求出
的值. (1)由两向量的坐标求出![]() 的坐标表示,把
的坐标表示,把![]() 和
和![]() 的值代入即可求出
的值代入即可求出![]() 的值;(2)把所求的式子利用两角和与差的余弦函数公式及特殊角的三角函数值化简后,将
的值;(2)把所求的式子利用两角和与差的余弦函数公式及特殊角的三角函数值化简后,将![]() 和
和![]() 的值代入即可求出值.
的值代入即可求出值.
试题解析:(1)因为a⊥b,所以a·b=4×3+5cos α×(-4tan α)=0,
解得sin α=![]() .又因为α∈(0,
.又因为α∈(0,![]() ),所以cos α=
),所以cos α=![]() ,tan α=
,tan α=![]() ,
,
所以a+b=(7,1),因此|a+b|=![]() .
.
(2)cos(α+![]() )=cos αcos
)=cos αcos![]() -sin αsin
-sin αsin![]() .
.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】
已知函数f(x)=x3+ax2+bx+c,曲线y=f(x)在点x=1处的切线方程为
l:y=3x+1,且当x=![]() 时,y=f(x)有极值.
时,y=f(x)有极值.
(1)求a,b,c的值;
(2)求y=f(x)在[-3,1]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“莞马”活动中的α机器人一度成为新闻热点,为检测其质量,从一生产流水线上抽取20件该产品,其中合格产品有15件,不合格的产品有5件.
(1)现从这20件产品中任意抽取2件,记不合格的产品数为X,求X的分布列及数学期望;
(2)用频率估计概率,现从流水线中任意抽取三个机器人,记ξ为合格机器人与不合格机器人的件数差的绝对值,求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为 ![]() ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为 ![]() ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为x,求x≤3的概率;
(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣alnx(a∈R)
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.
组号 | 分组 | 频数 |
1 |
| 2 |
2 |
| 8 |
3 |
| 7 |
4 |
| 3 |
(Ⅰ)现从融合指数在![]() 和
和![]() 内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在
内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在![]() 的概率;
的概率;
(Ⅱ)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
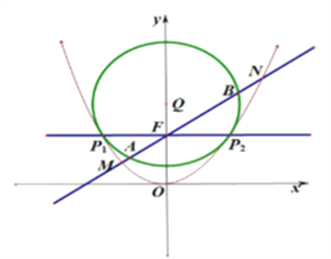
【题目】如图所示,曲线![]() 是以坐标原点
是以坐标原点![]() 为顶点,
为顶点, ![]() 轴为对称轴的抛物线,且焦点在
轴为对称轴的抛物线,且焦点在![]() 轴正半轴上,圆
轴正半轴上,圆![]() .过焦点
.过焦点![]() 且与
且与![]() 轴平行的直线与抛物线交于
轴平行的直线与抛物线交于![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)直线![]() 过
过![]() 且与抛物线
且与抛物线![]() 和圆
和圆![]() 依次交于
依次交于![]() ,且直线
,且直线![]() 的斜率
的斜率![]() ,求
,求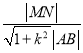 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 上异于长轴端点的两点.
上异于长轴端点的两点.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() :
: ![]() ,且
,且![]() ,垂足为
,垂足为![]() ,
, ![]() ,垂足为
,垂足为![]() ,若
,若![]() ,且
,且![]() 的面积是
的面积是![]() 面积的5倍,求
面积的5倍,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com