
����Ŀ�������ʱ��г���ǿ�ƽ��룬��������������������һҹ�����������鲼��һ���߳��еĴ��С��.Ϊ�˽��������![]() �е�ʹ�������ij���������������������ʾ����飬���Ӳ������������г�ȡ��200�˽��г����������õ�������λ���ˣ�
�е�ʹ�������ij���������������������ʾ����飬���Ӳ������������г�ȡ��200�˽��г����������õ�������λ���ˣ�
����ʹ�� | ż������ | �ϼ� | |
30�꼰���� | 70 | 30 | 100 |
30������ | 60 | 40 | 100 |
�ϼ� | 130 | 70 | 200 |
��1�������������ݣ��ܷ��ڷ�����ĸ��ʲ�����0.15��ǰ������Ϊ![]() ��ʹ�ù�����������������йأ�
��ʹ�ù�����������������йأ�
��2���ִ�����ȡ��30�����ϵ����������÷ֲ�����ķ����ٳ�ȡ5��.
��i���ֱ�����5���о���ʹ�á�ż�����ù���������������
��ii������5���У������ѡ��2������һ����Ʒ����ѡ����2����������1�˾���ʹ�ù��������ĸ���.
�ο���ʽ�� 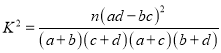 ������
������![]() .
.
�ο����ݣ�
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 3.841 | 5.024 | 6.635 |
���𰸡�(1)���ڷ�����ĸ��ʲ�����0.15��ǰ������Ϊ![]() ��ʹ�ù�����������������йأ�
��ʹ�ù�����������������йأ�
(2)(i)����ʹ�ù�����������3�ˣ�ż�����ù�����������2��.(ii) ![]()
�����������������
(1)���������ɵ�![]() ���������ڷ�����ĸ��ʲ�����0.15��ǰ������Ϊ
���������ڷ�����ĸ��ʲ�����0.15��ǰ������Ϊ![]() ��ʹ�ù�����������������й�.
��ʹ�ù�����������������й�.
(2)��i���������֪������ʹ�ù�����������![]() ���ˣ���ż�����ù�����������
���ˣ���ż�����ù�����������![]() ���ˣ�.
���ˣ�.
��ii���������г����п��ܵĽ������Ϲŵ����ʽ�Ͷ����¼���ʽ�ɵ�ѡ����2����������1�˾���ʹ�ù��������ĸ���![]() .
.
���������
��1������������֪��
![]() .
.
��Ϊ![]() ��
��
�������ڷ�����ĸ��ʲ�����0.15��ǰ������Ϊ![]() ��ʹ�ù�����������������й�.
��ʹ�ù�����������������й�.
��2����i���������֪������ȡ��5��30�����ϵ������У�����ʹ�ù�����������![]() ���ˣ���ż�����ù�����������
���ˣ���ż�����ù�����������![]() ���ˣ�.
���ˣ�.
��ii������5���У�����ʹ�ù���������3�˷ֱ�Ϊ![]() ��
�� ![]() ��
�� ![]() ��ż�����ù���������2�˷ֱ�Ϊ
��ż�����ù���������2�˷ֱ�Ϊ![]() ��
�� ![]() .
.
���5����ѡ��2�˵����п��ܽ��Ϊ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��10��.
��10��.
����û��1�˾���ʹ�ù��������Ŀ��ܽ��Ϊ![]() ��1�֣�
��1�֣�
��ѡ����2����������1�˾���ʹ�ù��������ĸ���![]() .
.


 ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������E:x2=2py(p>0) �Ľ���F��б�ʷֱ�Ϊ k1,k2 ��������ͬ��ֱ�� l1,l2 ����k1+k2=2 ��l1��E �ཻ�ڵ�A��B�� l2��E �ཻ�ڵ�C��D.��AB��CDΪֱ����ԲM��ԲN��M��NΪԲ�ģ��Ĺ��������ڵ�ֱ��Ϊ l .
��1����k1>0,k2>0 ��֤����![]() ��
��
��2������M��ֱ�� l �ľ������СֵΪ![]() ����������E�ķ���.
����������E�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��x+y+m=0��Բx2+y2=4���ڲ�ͬ������A��B��O������ԭ�㣬 ![]() ����ʵ��m��ȡֵ��Χ�ǣ� ��
����ʵ��m��ȡֵ��Χ�ǣ� ��
A.[��2��2]
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������ʵ��m��nΪ������������h��x������h��m+x��+h��m��x��=2n������y=h��x����ͼ����ڵ㣨m��n�������ĶԳơ���
��1����֪����f��x��= ![]() ��ͼ����ڵ㣨1��b�������ĶԳƣ���ʵ��b��ֵ��
��ͼ����ڵ㣨1��b�������ĶԳƣ���ʵ��b��ֵ��
��2����֪����g��x������g��2+x��+g����x��=4����x��[0��2]ʱ������g��x����3�������ҵ�x��[0��1]ʱ��g��x��=2k��x��1��+1 �� ��ʵ��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABC�У�PA��AB��PA��BC��AB��BC��PA��AB��BC��2��DΪ�߶�AC���е㣬EΪ�߶�PC��һ��.

(1)��֤��PA��BD��
(2)��֤��ƽ��BDE��ƽ��PAC��
(3)��PA��ƽ��BDEʱ��������E��BCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �Ƕ�����
�Ƕ�����![]() �ϵ��溯������
�ϵ��溯������![]() Ϊż��������
Ϊż��������![]() ʱ��
ʱ��![]() ��������
��������![]() ǡ��һ����㣬��ʵ��
ǡ��һ����㣬��ʵ��![]() ��ȡֵ�����ǣ� ��
��ȡֵ�����ǣ� ��
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�OAB�У���PΪ�߶�AB�ϵ�һ�����㣨�������˵㣩�������� ![]() =��
=�� ![]() ��
�� 
��1������= ![]() ��������
�������� ![]() ��
�� ![]() ��ʾ
��ʾ ![]() ��
��
��2����| ![]() |=4��|
|=4��| ![]() |=3���ҡ�AOB=60�㣬��
|=3���ҡ�AOB=60�㣬�� ![]()
![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l��y=ax+1��a��a��R����������ʵ��aʹ��һ��������ֱ��l��������ͬ�Ľ��㣬��������������Ϊ�˵���߶γ���ǡ�õ���|a|����ƴ�����Ϊֱ��l�ġ��������ߡ�����������������߷��̣���y=��2|x��1|����y=x2���ۣ�x��1��2+��y��1��2=1����x2+3y2=4��������ֱ��l�ġ��������ߡ��У� ��
A.�٢�
B.�ڢ�
C.�ڢ�
D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��̬����ƽ��ͼ�ʳ����Σ���ͼ������֪��̬���ij�AB=8��km������AD=4��km����M��N�ֱ�Ϊ������ABCD��AD��DC���е㣬P��QΪ������ABCD��AB��BC�������˵㣩�ϵ�һ�㣮�ֹ������������۹��P��Q��N��M��P��Ҫ��۹��Χ���ı��Σ���ͼ��Ӱ���֣������Ϊ15��km2������BP=x��km����BQ=y��km���� 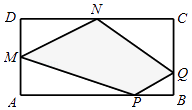
��1����д��y����x�ĺ�����ϵʽ�������x��ȡֵ��Χ��
��2����BΪ����ڣ�P��QΪ�۹վ���۹վPλ���߶�AB�������B��һ�࣮�����㣬ÿ����B������۹վP��Q�����۹���ο�������ȣ���Ϊ1���ˣ������ȷ���۹վP��Q��λ�ã�ʹ�����οͲ��о���֮�����������ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com