�⣺������֪��
��I����A={1��2������2
n-1����}��A��B�е�Ԫ�ذ���С�����˳���Ϊ{c
n}����c
n=n��n��N
*��
����c
n=n����Ϊ5��6��7∉A����5��6��7��B
��Ȳ�����{b
n}�Ĺ���Ϊ1������3������{b
n}�е����ˣ�3ֻ����������{b
n}�еĵ�1��2��3�
��b
1=3ʱ����b
n=n+2��
��b
2=3����b
n=n+1��
��b
3=3����b
n=n��
��II����i����ΪA={1��2������2
n-1����}��A��B�е�Ԫ�ذ���С�����˳���Ϊ{c
n}��
�Լ���{c
n}�е�Ԫ��2���з������ۣ�
�ٵ�c
2=2ʱ����{c
n}��ǰ5��ɵȱ����У���c
4=2
3=8=c
9����Ȼ��������
�ڵ�c
3=2ʱ����{c
n}��ǰ5��ɵȱ����У���b
12=2����b
1=

��
�������{c
n}��ǰ5��ֱ�Ϊ1��

��2��2

��4��
���� b
n=

n��������{c
n}��ǰ9��ֱ�Ϊ1��

��2��2

��4��3

��4

��5

��8���������з���Ҫ��
�۵�c
k=2��k��4��ʱ����b
2-b
1��2-1��������{b
n}����d��1��
��b
6=b
1+5d��2+5=7��1��2��4��c
9��
��1��2��4������{c
n}��ǰ8���У�����A��B=∅��������b
1��b
2������b
6�Լ�1��2��4��9�
���Ǿ�С��8��������{c
n}��ǰ9���С��8������c
9=8ì�ܣ�����Ҳ��������
����������b
n=

n��
��Σ���n��4ʱ��
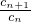
=

��

��
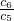
=
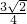
��

��
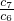
=

��

��
��n��7ʱ��c
n��4

����Ϊ{b
n}�ǹ���Ϊ

�ĵȲ����У����� c
n+1-c
n��

��
����
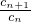
=
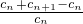
=1+
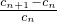
��1+
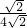
=

����ʱ��n������Ҫ��
���Է���Ҫ���nһ����5����
��ii��֤�����ɣ�i��֪������{c
n}��A��B�е�Ԫ�ذ���С�����˳���������ã�
��1��

��2��2

��4��3

��4

��5

��8������
�����������ԣ�m��n������m��nʱ����c
m��c
n��
��|c
n+1+c
m-c
n-c
m+1|��0��
��|c
n+1+c
m-c
n-c
m+1|=|��c
n+1-c
n��-��c
m+1-c
m��|��|c
n+1-c
n|+|c
m+1-c
m|��2|c
n+1-c
n|=2|

n��-2
n-1|��
��2|

n��-2
n-1|��

����|

n��-2
n-1|��
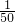
��
�������������������ԣ�m��n��ʹ�ò���ʽ
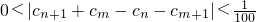
������
��������I��������֪����{a
n}��ͨ�ʽa
n=2
n-1������{b
n}�ǵȲ����У�����A��B�е�Ԫ�ذ���С�����˳�����й��ɵ����м�Ϊ{c
n}����c
n=n��n��N*����Ԫ��3��5��6��7���з������ó�����{b
n}�ǹ���Ϊ1�ĵȲ����У�����������ɣ�
��II����i����A��B=∅������{c
n}��ǰ5��ɵȱ����У���c
1=1��c
9=8����Ԫ��2���з������ۣ��Ӷ����
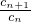
��

��������n�ĸ�����
��ii���ɣ�i��֪������{c
n}��A��B�е�Ԫ�ذ���С�����˳���������ã���1��

��2��2

��4��3

��4

��5

��8������Ȼ�����þ���ֵ����ʽ����֤�����ɣ�
���������⿼���˵Ȳ����к͵ȱ����е��ۺ����ã���Ԫ��2���÷������۵ķ����������{b
n}��ͨ�ʽ�����ַ������۵�˼�룻���ڣ�II����̽�֣����˷����������⣬�������˷�֤��������⣬�����˷���������ԣ���������Ŀ���Ѷȣ������⣮

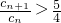 ��������n�ĸ�����
��������n�ĸ�����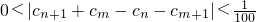 ������
������ ��
�� ��2��2
��2��2 ��4��
��4�� n��������{cn}��ǰ9��ֱ�Ϊ1��
n��������{cn}��ǰ9��ֱ�Ϊ1�� ��2��2
��2��2 ��4��3
��4��3 ��4
��4 ��5
��5 ��8���������з���Ҫ��
��8���������з���Ҫ�� n��
n��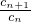 =
= ��
�� ��
��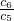 =
=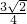 ��
�� ��
��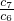 =
= ��
�� ��
�� ����Ϊ{bn}�ǹ���Ϊ
����Ϊ{bn}�ǹ���Ϊ �ĵȲ����У����� cn+1-cn��
�ĵȲ����У����� cn+1-cn�� ��
��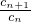 =
=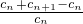 =1+
=1+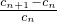 ��1+
��1+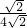 =
= ����ʱ��n������Ҫ��
����ʱ��n������Ҫ�� ��2��2
��2��2 ��4��3
��4��3 ��4
��4 ��5
��5 ��8������
��8������ n��-2n-1|��
n��-2n-1|�� n��-2n-1|��
n��-2n-1|�� ����|
����| n��-2n-1|��
n��-2n-1|��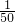 ��
��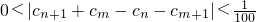 ������
������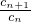 ��
�� ��������n�ĸ�����
��������n�ĸ����� ��2��2
��2��2 ��4��3
��4��3 ��4
��4 ��5
��5 ��8������Ȼ�����þ���ֵ����ʽ����֤�����ɣ�
��8������Ȼ�����þ���ֵ����ʽ����֤�����ɣ�

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�