解:(1)函数f(x)在[-1,1]上单调增,证明如下
由题意,设x
1,x
2∈[-1,1],且x
1<x
2则x
1-x
2<0
∵x,y∈[-1,1],x+y≠0有(x+y)•[f(x)+f(y)]>0.
令x=x
1,y=-x
2,
∴f(x
1)+f(-x
2)<0
∵函数f(x)是定义在[-1,1]上的奇函数
∴f(x
1)-f(x
2)<0
∴函数f(x)在[-1,1]上单调增;
(2)由(1)知,
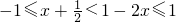
,解得:
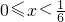
(3)由于函数f(x)在[-1,1]上单调增,
∴函数f(x)在[-1,1]上的最大值为f(1)=1
∴f(x)≤m
2-2am+1对所有x∈[-1,1],a∈[-1,1]恒成立可转化为:0≤m
2-2am对所有a∈[-1,1]恒成立
∴
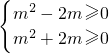
,
解得m≥2或m≤-2或m=0
分析:(1)设x
1,x
2∈[-1,1],且x
1<x
2,则x
1-x
2<0,利用x,y∈[-1,1],x+y≠0有(x+y)•[f(x)+f(y)]>0,可得f(x
1)+f(-x
2)<0,根据函数f(x)是定义在[-1,1]上的奇函数,即可得函数f(x)在[-1,1]上单调增;
(2)由(1)知,
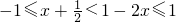
,解之即可;
(3)先确定函数f(x)在[-1,1]上的最大值为f(1)=1,将f(x)≤m
2-2am+1对所有x∈[-1,1],a∈[-1,1]恒成立转化为:0≤m
2-2am对所有a∈[-1,1]恒成立,从而可求实数m的取值范围.
点评:本题以抽象函数的性质为载体,考查函数的单调性,考查单调性与奇偶性的结合,同时考查了恒成立问题,解题的关键是:f(x)≤m
2-2am+1对所有x∈[-1,1],a∈[-1,1]恒成立转化为:0≤m
2-2am对所有a∈[-1,1]恒成立

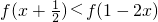 ;
;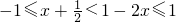 ,解得:
,解得: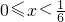
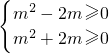 ,
,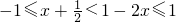 ,解之即可;
,解之即可;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 已知函数f(x)=x+
已知函数f(x)=x+