

 ]•an2=q,(其中q≥2010),an的前n项和为Sn,
]•an2=q,(其中q≥2010),an的前n项和为Sn, ,若bn≥2011n恒成立,求q的最小值.
,若bn≥2011n恒成立,求q的最小值. ,知
,知 =
= ,x>0.由f(x)在[1,+∞)上为增函数,知x∈[1,+∞)时,
,x>0.由f(x)在[1,+∞)上为增函数,知x∈[1,+∞)时, 恒成立.由此能导出m的范围.
恒成立.由此能导出m的范围. ,x∈[1,+∞)时,
,x∈[1,+∞)时, ,f(x)在[1,+∞)上单调递增,要比较f(aaba4a)与f[(a+b)a+b]的大小,即比较
,f(x)在[1,+∞)上单调递增,要比较f(aaba4a)与f[(a+b)a+b]的大小,即比较 与
与 的大小.由此能推导出f(aabb4a)>f[(a+b)a+b].
的大小.由此能推导出f(aabb4a)>f[(a+b)a+b]. ,且
,且 ,所以
,所以 ,由
,由 恒成立,q≥2010时,数列
恒成立,q≥2010时,数列 为单调递减数列,能够推导出若bn≥2011n恒成立,求q的最小值.
为单调递减数列,能够推导出若bn≥2011n恒成立,求q的最小值. ,
,
 ,x>0.
,x>0. 在[1,+∞)上恒大于或等于0,
在[1,+∞)上恒大于或等于0, 恒成立.
恒成立. 恒成立.
恒成立. ,x∈[1,+∞)时,
,x∈[1,+∞)时, ,
, 与
与 的大小.
的大小. -
-
 -
-
 .
. ,
, ,
, ,
, ,
, ,
, .
. =
= ,q≥2010,
,q≥2010, 恒成立,
恒成立, 为单调递减数列,
为单调递减数列, ,
, 中的每一项都大于2011,
中的每一项都大于2011, 恒成立,
恒成立, 为单调递减数列,
为单调递减数列, ,
, 在有限项后必定小于2011,
在有限项后必定小于2011, ,
, 中必有一项,
中必有一项, ,(其中Mk≥0,且Mk+1<0),
,(其中Mk≥0,且Mk+1<0), +…+
+…+
 ,
, 中必有一项,(设为第k项)
中必有一项,(设为第k项) ,(其中Mk≥0,且Mk+1<0)的推导过程.
,(其中Mk≥0,且Mk+1<0)的推导过程. 

科目:高中数学 来源: 题型:
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
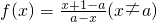
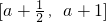 时,求f(x)的值域;
时,求f(x)的值域;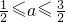 ,求g(x)的最小值.
,求g(x)的最小值.查看答案和解析>>
科目:高中数学 来源:徐州模拟 题型:解答题
| 2 |
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com