
 亩水稻,
亩水稻, 亩花生时,能获得最大利润,最大利润为1650元.
亩花生时,能获得最大利润,最大利润为1650元. 亩水稻,
亩水稻, 亩花生时,能获得利润
亩花生时,能获得利润 元.则
元.则 即
即
 即
即 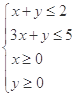

 ,在可行域内平移直线
,在可行域内平移直线 ,可知当直线过点
,可知当直线过点 时,纵截距
时,纵截距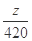 有最大值,
有最大值,  解得
解得 ,
, ,
, 时,
时,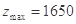 元,
元, 亩水稻,
亩水稻, 亩花生时,能获得最大利润,最大利润为1650元.
亩花生时,能获得最大利润,最大利润为1650元. 

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com