
【题目】下表是检测某种浓度的农药随时间x(秒)渗入某种水果表皮深度y(微米)的一组结果.
时间x(秒) | 5 | 10 | 15 | 20 | 30 |
深度y(微米) | 6 | 10 | 10 | 13 | 16 |
(1)在规定的坐标系中,画出 x,y 的散点图; 
(2)求y与x之间的回归方程,并预测40秒时的深度(回归方程精确到小数点后两位;预测结果精确到整数). 回归方程: ![]() =bx+a,其中
=bx+a,其中 ![]() =
=  ,a=
,a= ![]() ﹣b
﹣b ![]() .
.
【答案】
(1)解:在规定的坐标系中,画出 x,y 的散点图如图所示; 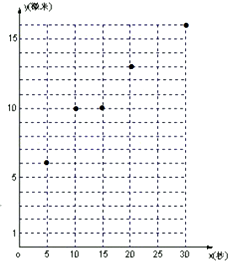
(2)解:计算 ![]() =
= ![]() ×(5+10+15+20+30)=16,
×(5+10+15+20+30)=16,
![]() =
= ![]() ×(6+10+10+13+16)=11;
×(6+10+10+13+16)=11;
![]() xiyi=5×6+10×10+15×10+20×13+30×16=1020,
xiyi=5×6+10×10+15×10+20×13+30×16=1020,
![]() =52+102+152+202+302=1650,
=52+102+152+202+302=1650,
∴回归系数为: ![]() =
= 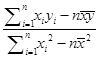 =
= ![]() ≈0.53,
≈0.53,
a= ![]() ﹣b
﹣b ![]() =11﹣0.53×16=2.52;
=11﹣0.53×16=2.52;
∴回归方程为: ![]() =0.53x+2.52;
=0.53x+2.52;
当x=40时, ![]() =0.53×40+2.52=23.72,
=0.53×40+2.52=23.72,
即预测40秒时的深度23.72微米.
【解析】(1)在规定的坐标系中,画出 x,y 的散点图即可;(2)计算 ![]() 、
、 ![]() ,求出回归系数
,求出回归系数 ![]() 、a,
、a,
写出回归方程,计算x=40时 ![]() 的值即可.
的值即可.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点. 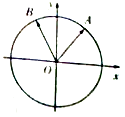
(I)若A,B两点的纵会标分别为 ![]() 的值;
的值;
(II)已知点C是单位圆上的一点,且 ![]() 的夹角θ.
的夹角θ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2是椭圆 ![]() +
+ ![]() =1的左、右焦点,O为坐标原点,点P(﹣1,
=1的左、右焦点,O为坐标原点,点P(﹣1, ![]() )在椭圆上,线段PF2与y轴的交点M满足
)在椭圆上,线段PF2与y轴的交点M满足 ![]() +
+ ![]() =
= ![]() ;
;
(1)求椭圆的标准方程;
(2)⊙O是以F1F2为直径的圆,一直线l:y=kx+m与⊙O相切,并与椭圆交于不同的两点A、B.当 ![]() =λ且满足
=λ且满足 ![]() ≤λ≤
≤λ≤ ![]() 时,求△AOB面积S的取值范围.
时,求△AOB面积S的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的方程为:ax2+ay2﹣2a2x﹣4y=0(a≠0,a为常数).
(1)判断曲线C的形状;
(2)设曲线C分别与x轴、y轴交于点A、B(A、B不同于原点O),试判断△AOB的面积S是否为定值?并证明你的判断;
(3)设直线l:y=﹣2x+4与曲线C交于不同的两点M、N,且|OM|=|ON|,求曲线C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数f(x)=3sin(2x+φ)的图象关于点( ![]() ,0)成中心对称(|φ|<
,0)成中心对称(|φ|< ![]() ),那么函数f(x)图象的一条对称轴是( )
),那么函数f(x)图象的一条对称轴是( )
A.x=﹣ ![]()
B.x= ![]()
C.x= ![]()
D.x= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,若存在常数T≠0,使得f(x)=Tf(x+T)对任意的x∈R成立,则称函数f(x)是Ω函数. (Ⅰ)判断函数f(x)=x,g(x)=sinπx是否是Ω函数;(只需写出结论)
(Ⅱ)说明:请在(i)、(ii)问中选择一问解答即可,两问都作答的按选择(i)计分
(i)求证:若函数f(x)是Ω函数,且f(x)是偶函数,则f(x)是周期函数;
(ii)求证:若函数f(x)是Ω函数,且f(x)是奇函数,则f(x)是周期函数;
(Ⅲ)求证:当a>1时,函数f(x)=ax一定是Ω函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com