
| b |
| x |
| b |
| x2 |
| 1 |
| 2 |
| a-2 |
| x |
| a-2 |
| x2 |
| 2 |
| x |
a(x-1)(x-
| ||
| x2 |
| b |
| x |
| b |
| x2 |
| b |
| x |
| 1 |
| 2 |
| a-2 |
| x |
| a-2 |
| x |
| a-2 |
| x2 |
| 2 |
| x |
| ax2-2x-(a-2) |
| x2 |
a(x-1)(x-
| ||
| x2 |
| 2-a |
| a |
| 2-a |
| a |
| 2-a |
| a |
| 2-a |
| a |


科目:高中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某厂生产一种内径为105mm的零件,为了检查该生产流水线的质量情况,随机抽取该流水线上50个零件作为样本测出它们的内径长度(单位:mm),长度的分组区间为[90,95),[95,100),[100,105),[105,110),[110,115),由此得到样本的频率分布直方图,如图所示.已知内径长度在[100,110)之间的零件被认定为一等品,在[95,100)或[110,115)之间的零件被认定为二等品,否则认定为次品.
某厂生产一种内径为105mm的零件,为了检查该生产流水线的质量情况,随机抽取该流水线上50个零件作为样本测出它们的内径长度(单位:mm),长度的分组区间为[90,95),[95,100),[100,105),[105,110),[110,115),由此得到样本的频率分布直方图,如图所示.已知内径长度在[100,110)之间的零件被认定为一等品,在[95,100)或[110,115)之间的零件被认定为二等品,否则认定为次品.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图是调查某地某公司1000名员工的月收入后制作的直方图.根据直方图估计:
如图是调查某地某公司1000名员工的月收入后制作的直方图.根据直方图估计:查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
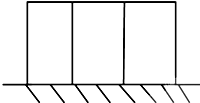 用长度为20m的篱笆围建一个一面靠墙的矩形鸡舍,且鸡舍内用相同的篱笆隔成三间(如图所示),如果挨着墙的边长为x,鸡舍面积为y
用长度为20m的篱笆围建一个一面靠墙的矩形鸡舍,且鸡舍内用相同的篱笆隔成三间(如图所示),如果挨着墙的边长为x,鸡舍面积为y查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com