
下图是一几何体的直观图、正(主)视图、侧(左)视图、俯视图
(1)若 为
为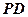 的中点,求证
的中点,求证 :
: 平面
平面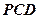 ;
;
(2)求平面 与平面
与平面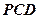 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
科目:高中数学 来源: 题型:解答题
(12分)如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,
总计耗用9.6米铁丝,再用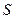 平方米塑料片制成圆柱的侧面和下底面(不安装上底面)。
平方米塑料片制成圆柱的侧面和下底面(不安装上底面)。
(Ⅰ)当圆柱底面半径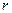 取何
取何 值时,
值时,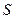 取得最大值?并求出该最大值(结果精确到0.01平方米);
取得最大值?并求出该最大值(结果精确到0.01平方米);
(Ⅱ)若要制作一个如图放置的,底面半径为0.3米的灯笼,请作出用于灯笼的三视图(作图时,不需考虑骨架等因素)。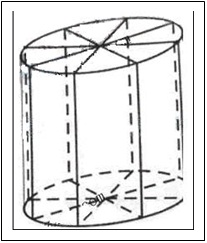
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图1,在平面内,ABCD 是
是 且
且 的菱形,
的菱形, 和
和 都是正方形。将两个正方形分别沿AD,CD折起,使
都是正方形。将两个正方形分别沿AD,CD折起,使 与
与 重合于点D1。设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设
重合于点D1。设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设 (图2)。
(图2)。

(1)设二面角E – AC – D1的大小为q,若 ,求
,求 的取值范围;
的取值范围;
(2)在线段 上是否存在点
上是否存在点 ,使平面
,使平面 平面
平面 ,若存在,求出
,若存在,求出 分
分 所成的比
所成的比 ;若不存在,请说明理由。
;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)设圆台的高为3,其轴截面(过圆台轴的截面)如图
所示,母线A1A与 底面圆的直径AB的夹角为
底面圆的直径AB的夹角为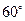 ,在轴截面中
,在轴截面中
A1B⊥A1A,求圆台的体积V.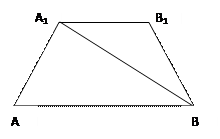
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
((本小题满分12分)
如图,多面体ABCD—EFG中,底面ABCD为正方形,GD//FC//AE,AE⊥平面ABCD,其正视图、俯视图如下: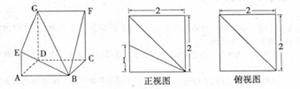
(I)求证:平面AEF⊥平面BDG;
(II)若存在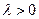 使得
使得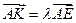 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为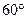 ,求
,求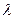 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com