
【题目】如图在△ABC中,已知点D在BC边上,满足AD⊥AC,cos ∠BAC=-![]() ,AB=3
,AB=3![]() ,BD=
,BD=![]() .
.
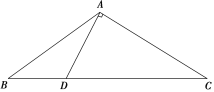
(1)求AD的长;
(2)求△ABC的面积.
【答案】见解析
【解析】(1)因为AD⊥AC,cos ∠BAC=-![]() ,
,
所以sin ∠BAC=![]() .
.
又sin ∠BAC=sin![]() =cos ∠BAD=
=cos ∠BAD=![]() ,
,
在△ABD中,BD2=AB2+AD2-2AB·AD·cos ∠BAD,
即AD2-8AD+15=0,
解得AD=5或AD=3,由于AB>AD,
所以AD=3.
(2)在△ABD中,![]() =
=![]() ,
,
又由cos ∠BAD=![]() 得sin ∠BAD=
得sin ∠BAD=![]() ,所以sin ∠ADB=
,所以sin ∠ADB=![]() ,则sin ∠ADC=sin(π-∠ADB)=sin ∠ADB=
,则sin ∠ADC=sin(π-∠ADB)=sin ∠ADB=![]() .
.
因为∠ADB=∠DAC+∠C=![]() +∠C,所以cos ∠C=
+∠C,所以cos ∠C=![]() .
.
在Rt△ADC中,cos ∠C=![]() ,则tan ∠C=
,则tan ∠C=![]() =
=![]() =
=![]() ,
,
所以AC=3![]() ,
,
则△ABC的面积S=![]() AB·AC·sin ∠BAC=
AB·AC·sin ∠BAC=![]() ×3
×3![]() ×3
×3![]() ×
×![]() =6
=6![]() .
.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳远 (单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳绳 (单位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a-1 | b | 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则( )
A. 2号学生进入30秒跳绳决赛 B. 5号学生进入30秒跳绳决赛
C. 8号学生进入30秒跳绳决赛 D. 9号学生进入30秒跳绳决赛
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,嵩山上原有一条笔直的山路BC,现在又新架设了一条索道AC,小李在山脚B处看索道AC,发现张角∠ABC=120°;从B处攀登400米到达D处,回头看索道AC,发现张角∠ADC=150°;从D处再攀登800米方到达C处,则索道AC的长为________米.
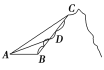
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一个圆柱形乒乓球筒,高为![]() 厘米,底面半径为
厘米,底面半径为![]() 厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度忽略不计).一个平面与两乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )
厘米.球筒的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度忽略不计).一个平面与两乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 的左,右顶点分别为
的左,右顶点分别为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() 的面积是
的面积是![]() 的面积的3倍.
的面积的3倍.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 与
与![]() 轴垂直,
轴垂直,![]() 是椭圆
是椭圆![]() 上位于直线
上位于直线![]() 两侧的动点,且满足
两侧的动点,且满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() sinωx·cosωx-cos2ωx(ω>0)的最小正周期为
sinωx·cosωx-cos2ωx(ω>0)的最小正周期为![]() .
.
(1)求ω的值;
(2)在△ABC中,sinB,sinA,sinC成等比数列,求此时f(A)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①点P(-1,4)到直线3x+4y =2的距离为3.
②过点M(-3,5)且在两坐标轴上的截距互为相反数的直线方程为![]() .
.
③命题“x∈R,使得x2﹣2x+1<0”的否定是真命题;
④“x ≤1,且y≤1”是“x + y ≤2”的充要条件.
其中不正确命题的序号是 _______________ .(把你认为不正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中错误的是( )
A. 在一次试卷分析中,从每个考室中抽取第5号考生的成绩进行统计,不是简单随机抽样
B. 对一个样本容量为100的数据分组,各组的频数如下:
区间 |
|
|
|
|
|
|
|
|
频数 | 1 | 1 | 3 | 3 | 18 | 16 | 28 | 30 |
估计小于29的数据大约占总体的![]()
C. 设产品产量与产品质量之间的线性相关系数为![]() ,这说明二者存在着高度相关
,这说明二者存在着高度相关
D. 通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如表列联表.
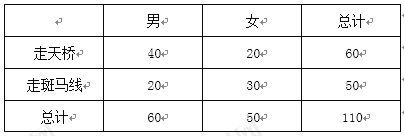
由![]() ,则有
,则有![]() 以上的把握认为“选择过马路方式与性别有关”
以上的把握认为“选择过马路方式与性别有关”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com