
【题目】已知函数 ![]() .
.
(1)判断并证明函数f(x)的奇偶性
(2)判断并证明当x∈(﹣1,1)时函数f(x)的单调性;
(3)在(2)成立的条件下,解不等式f(2x﹣1)+f(x)<0.
【答案】
(1)解:∵y=x2+1为偶函数,y=x为奇函数
根据函数奇偶性的性质,我们易得
函数 ![]() 为奇函数
为奇函数
(2)解:当x∈(﹣1,1)时
∵函数 ![]()
f'(x)= ![]() >0恒成立
>0恒成立
故f(x)在区间(﹣1,1)上为单调增函数
(3)解:在(2)成立的条件下,不等式f(2x﹣1)+f(x)<0可化为:
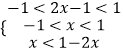
解得: ![]()
∴不等式的解集为 ![]()
【解析】(1)由于函数的定义域为R,关于原点对称,故我们可利用函数奇偶性的性质判断方法来解答问题;(2)由函数f(x)的解析式,我们易求出原函数的导函数的解析式,结合x∈(﹣1,1),确定导函数的符号,即可判断函数的单调性;(3)结合(1)、(2)的结论,我们可将原不等式转化为一个关于x的不等式组,解不等式组即可得到答案.
【考点精析】掌握函数单调性的判断方法和函数单调性的性质是解答本题的根本,需要知道单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=kx,g(x)= ![]() .
.
(1)求函数g(x)= ![]() 的单调区间;
的单调区间;
(2)若不等式f(x)≥g(x)在区间(0,+∞)上恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,抛物线
,抛物线![]() 的焦点均在
的焦点均在![]() 轴上,
轴上, ![]() 的中心和
的中心和![]() 的顶点均为原点
的顶点均为原点![]() ,从每条曲线上各取两个点,其坐标分别是
,从每条曲线上各取两个点,其坐标分别是![]() ,
, ![]() ,
, ![]() ,
, 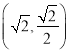 .
.
(1)求![]() ,
, ![]() 的标准方程;
的标准方程;
(2)是否存在直线![]() 满足条件:①过
满足条件:①过![]() 的焦点
的焦点![]() ;②与
;②与![]() 交于不同的两点
交于不同的两点![]() 且满足
且满足![]() ?若存在,求出直线方程;若不存在,请说明理由.
?若存在,求出直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1棱长为1,P、Q分别是线段AD1和BD上的点,且D1P:PA=DQ:QB=5:12, 
(1)求线段PQ的长度;
(2)求证PQ⊥AD;
(3)求证:PQ∥平面CDD1C1 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com