(本小题满分12分)已知
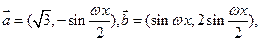
,函数
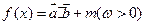
的最小正周期为
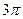
,且当

时,
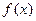
的最小值为0.
(1)求
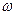
和
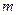
的值;
(2)在
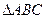
中,角

、

、
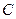
的对边分别是
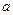
、
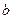
、
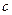
,满足
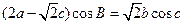
,求
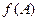
的取值范围.
(1)
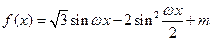



…………………3分

∵
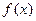
的最小值周期为
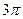
,故

∴

…………………4分

∵

∴

∴
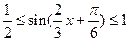
……………………5分
∴函数
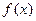
的最小值为

…………………6分
∴

∴
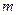
=0
(2)∵

∴

…………………8分
∴

…………………9分
∵
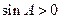
,∴

,∴

…………………10分
∴
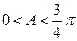
∴

……………………11分
∴

∵

∴

……………………12分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
设数列
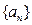
的前
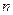
项和为
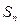
,对一切
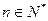
,点
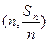
都在函数

图像上,设
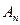
为数列
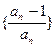
的前
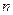
项积,是否存在实数
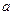
,使得
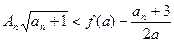
对一切
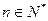
都成立?若存在,求出
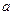
的范围,若不存在,请说明理由
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
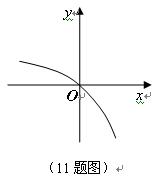
已知函数
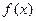
的定义域为
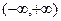
,
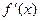
为
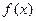
的导函数,函数
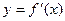
的图象如右图所示,且
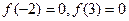
,则不 等式
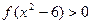
的解集为
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
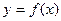
的定义域为R,且当
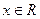
时,
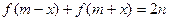
恒成立,
(1)求证:
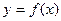
的图象关于点
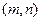
对称;
(2)求函数
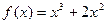
图象的一个对称点。
查看答案和解析>>

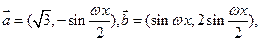 ,函数
,函数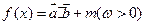 的最小正周期为
的最小正周期为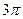 ,且当
,且当 时,
时,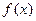 的最小值为0.
的最小值为0.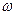 和
和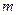 的值;
的值;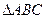 中,角
中,角 、
、 、
、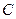 的对边分别是
的对边分别是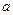 、
、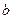 、
、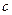 ,满足
,满足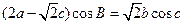 ,求
,求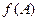 的取值范围.
的取值范围.