
【题目】已知f(x+1)= ![]() ,则f(2x﹣1)的定义域为( )
,则f(2x﹣1)的定义域为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:令x+1=t,则x=t﹣1,∴f(t)= ![]() =
= ![]() ,
,
∵﹣t2+2t≥0,解之得0≤t≤2.
∴函数f(t)= ![]() 的定义域为[0,2].
的定义域为[0,2].
令0≤2x﹣1≤2,解得 ![]() ,
,
∴函数f(2x﹣1)的定义域为[ ![]() ,
, ![]() ].
].
故选D.
【考点精析】根据题目的已知条件,利用函数的定义域及其求法的相关知识可以得到问题的答案,需要掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.


科目:高中数学 来源: 题型:
【题目】随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明,得到如下列联表:
男 | 女 | 总计 | |
读营养说明 | 16 | 8 | 24 |
不读营养说明 | 4 | 12 | 16 |
总计 | 20 | 20 | 40 |
(1)根据以上列联表进行独立性检验,能否在犯错误的概率不超过0.01的前提下认为性别与是否读营养说明之间有关系?
(2)从被询问的16名不读营养说明的大学生中,随机抽取2名学生,求抽到男生人数![]() 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
(注:  ,其中
,其中![]() 为样本容量)
为样本容量)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线 ![]() :
: 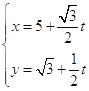 (t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为
(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为 ![]() .
.
(1)将曲线C的极坐标方程化为直坐标方程;
(2)设点M的直角坐标为 ![]() ,直线l与曲线C的交点为A,B,求|MA||MB|的值.
,直线l与曲线C的交点为A,B,求|MA||MB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系 ![]() 中,直线
中,直线 ![]() 的参数方程为
的参数方程为 ![]() 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点 ![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴的极坐标系下,圆
轴的非负半轴为极轴的极坐标系下,圆 ![]() 的方程为
的方程为 ![]() .
.
(1)求直线 ![]() 的普通方程和圆
的普通方程和圆 ![]() 的圆心的极坐标;
的圆心的极坐标;
(2)设直线 ![]() 和圆
和圆 ![]() 的交点为
的交点为 ![]() 、
、 ![]() ,求弦
,求弦 ![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点
的左焦点![]() 的离心率为
的离心率为![]() 是
是![]() 和
和![]() 的等比中项.
的等比中项.
(1)求曲线![]() 的方程;
的方程;
(2)倾斜角为![]() 的直线过原点
的直线过原点![]() 且与
且与![]() 交于
交于![]() 两点,倾斜角为
两点,倾斜角为![]() 的直线过
的直线过![]() 且与
且与![]() 交于
交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证: 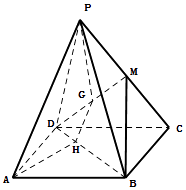
(1)AP∥平面BDM;
(2)AP∥GH.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com