
【题目】![]() 的内角
的内角![]() 的对边分别为
的对边分别为![]() ,已知
,已知![]() .
.
(1)求![]() ;
;
(2)若![]() ,
, ![]() 成等差数列,求
成等差数列,求![]() 的面积.
的面积.
【答案】(1) B=![]() (2)
(2) ![]()
【解析】试题分析:
(1)利用正弦定理把已知条件化为角的关系,再由诱导公式得![]() ,由两角和的正弦公式化简后可得
,由两角和的正弦公式化简后可得![]() 的正切值,从而得B角大小;
的正切值,从而得B角大小;
(2)利用余弦定理及等差数列的性质可得![]() 的方程组,解得
的方程组,解得![]() 后可得面积.
后可得面积.
试题解析:
(Ⅰ)由![]() a-
a-![]() bcosC=csinB及正弦定理得,
bcosC=csinB及正弦定理得,
![]() sinA-
sinA-![]() sinBcosC=sinCsinB,
sinBcosC=sinCsinB,
因为sinA=sin(B+C)=sinBcosC+sinCcosB,
所以![]() sinCcosB=sinCsinB.
sinCcosB=sinCsinB.
因为sinC≠0,所以tanB=![]() ,
,
又因为B为三角形的内角,
所以B=![]() .
.
(Ⅱ)由a,b,c成等差数列得a+c=2b=4,
由余弦定理得a2+c2-2accosB=b2,
即a2+c2-ac=4,
所以(a+c)2-3ac=4,从而有ac=4.
故S△ABC=![]() acsinB=
acsinB=![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱椎![]() 中,
中, ![]() 是棱
是棱![]() 上一点,且
上一点,且![]() ,底面
,底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 为正三角形,且平面
为正三角形,且平面![]() 平面
平面![]() ,平面
,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
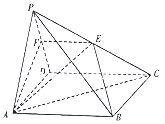
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个调查小组在对人们的休闲方式的一次调查中,共调查了150人,其中男性45人,女性55人。女性中有35人主要的休闲方式是室内活动,另外20人主要的休闲方式是室外运动;男性中15人主要的休闲方式是室内活动,另外30人主要的休闲方式是室外运动。
参考数据:![]()
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)根据以上数据建立一个![]() 的列联表;
的列联表;
(2)能否在犯错误的概率不超过0.005的前提下认为休闲方式与性别有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.![]() 为
为![]() 的右焦点,
的右焦点,![]() 为
为![]() 上一点,
上一点,![]() 轴,
轴,![]() 的半径为
的半径为![]() .
.
(1)求![]() 和
和![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点,其中
两点,其中![]() 在第一象限,是否存在
在第一象限,是否存在![]() 使
使![]() ?若存在,求
?若存在,求![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2α﹣4cosα=0.已知直线l的参数方程为![]() (
(![]() 为参数),点M的直角坐标为
为参数),点M的直角坐标为![]() .
.
(1)求直线l和曲线C的普通方程;
(2)设直线l与曲线C交于A,B两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com