
分析 (1)根据题意和${a}_{n}=\left\{\begin{array}{l}{{s}_{1},n=1}\\{{s}_{n}-{s}_{n-1},n≥2}\end{array}\right.$,分别列出式子化简、验证后求出an;
(2)由(1)化简和对数的运算法则化简bn=log2$\frac{{a}_{n+2}}{7}$,代入cn=$\frac{{b}_{n}}{{2}^{n+1}}$化简,利用错位相减法和等比数列的前n项和公式求出前n项和Tn,即可求出答案.
解答 解:(1)由题意得,a1=1,an=3Sn-1+4(n≥2),
当n=2时,a2=3S1+4=7,
当n≥2时,由an=3Sn-1+4(n≥2),得an+1=3Sn+4,
两式相减得,an+1=4an(n≥2),
∴数列{an}从第二项起是以4为公比、7为首项的等比数列,
则${a}_{n}={a}_{2}×{4}^{n-2}=7×{4}^{n-2}$(n≥2),此时对n=1不成立,
∴${a}_{n}=\left\{\begin{array}{l}{1,n=1}\\{7×{4}^{n-2},n≥2}\end{array}\right.$;
(2)由(1)得,bn=log2$\frac{{a}_{n+2}}{7}$=${log}_{2}^{{4}^{n}}$=2n,
则cn=$\frac{{b}_{n}}{{2}^{n+1}}$=$\frac{n}{{2}^{n}}$,
∴${T}_{n}=\frac{1}{2}+\frac{2}{{2}^{2}}+\frac{3}{{2}^{3}}+…+\frac{n}{{2}^{n}}$,①
$\frac{1}{2}{T}_{n}=\frac{1}{{2}^{2}}+\frac{2}{{2}^{3}}+\frac{3}{{2}^{4}}+…+\frac{n}{{2}^{n+1}}\$,②
①-②得,$\frac{1}{2}{T}_{n}=\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}}-\frac{n}{{2}^{n+1}}$
=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n+1}}$=$1-\frac{n+2}{{2}^{n+1}}$,
∴${T}_{n}=2-\frac{n+2}{{2}^{n}}$,即${T}_{n}+\frac{n+2}{{2}^{n}}=2$.
点评 本题考查了等比数列的通项公式、前n项和公式,以及${a}_{n}=\left\{\begin{array}{l}{{s}_{1},n=1}\\{{s}_{n}-{s}_{n-1},n≥2}\end{array}\right.$的应用,考查了错位相减法求数列的和,化简、变形能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m⊥n | B. | m∥n | C. | m与n相交 | D. | m与n异面 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
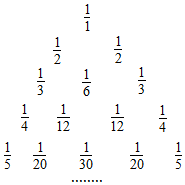 如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数之和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,则第n(n≥4)行倒数第四个数(从右往左数)为$\frac{1}{{n•C_{n-1}^3}}$或$\frac{6}{n(n-1)(n-2)(n-3)}$.
如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数之和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,则第n(n≥4)行倒数第四个数(从右往左数)为$\frac{1}{{n•C_{n-1}^3}}$或$\frac{6}{n(n-1)(n-2)(n-3)}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 为偶函数 | B. | 为奇函数 | ||
| C. | 既为奇函数又为偶函数 | D. | 为非奇非偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 228 | B. | 240 | C. | 260 | D. | 273 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
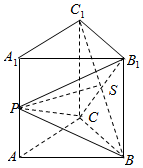 已知直三棱柱ABC-A1B1C1的各棱长均为a,点P是侧棱AA1的中点,BC1∩B1C=S
已知直三棱柱ABC-A1B1C1的各棱长均为a,点P是侧棱AA1的中点,BC1∩B1C=S查看答案和解析>>
科目:高中数学 来源: 题型:解答题
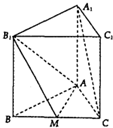 如图,三棱柱ABC-A1B1C1的所有棱长都为1,且侧棱与底面垂直,M是BC的中点.
如图,三棱柱ABC-A1B1C1的所有棱长都为1,且侧棱与底面垂直,M是BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com