
分析 由题意求出a=2,然后求出对数型函数的定义域,根据内函数t=x2-2x-3在(-∞,-1)上为减函数,结合复合函数的单调性可得原复合函数的单调减区间.
解答 解:∵幂函数y=xa过点(2,4),
∴2a=4,即a=2.
则函数y=loga(x2-2x-3)=$lo{g}_{a}({x}^{2}-2x-3)$.
由x2-2x-3>0,解得:x<-1或x>3.
∴函数y=$lo{g}_{2}({x}^{2}-2x-3)$的定义域为(-∞,-1)∪(3,+∞),
函数t=x2-2x-3在(-∞,-1)上为减函数,
而外函数y=log2t为定义域内的增函数,
∴函数y=loga(x2-2x-3)的单调减区间为(-∞,-1).
故答案为:(-∞,-1).
点评 本题考查复合函数的单调性,复合的两个函数同增则增,同减则减,一增一减则减,注意对数函数的定义域是求解的前提,考查学生发现问题解决问题的能力,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | $y=1o{g_{\frac{1}{2}}}x$ | B. | y=2x | C. | $y=\frac{1}{x}$ | D. | $y={x^{-\frac{2}{3}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 气温/(℃) | 4 | 2 | 1 | -1 | -3 |
| 杯数 | 24 | 36 | 40 | 49 | 61 |
| A. | y=4x+36 | B. | y=5x+20 | C. | y=-4x+44 | D. | y=-5x+45 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -$\frac{1}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2014 | B. | -2015 | C. | -2013 | D. | -2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
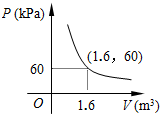 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3) 的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3) 的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )| A. | 不小于$\frac{5}{4}$m3 | B. | 小于$\frac{5}{4}$m3 | C. | 不小于$\frac{4}{5}$m3 | D. | 不大于$\frac{4}{5}$m3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com