练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    异面直线a，b所成的角为60°，则过空间中一点P与a，b都成30°的直线有    条？与a，b都成50°的直线有    条？与a，b都成60°的直线有    条？与a，b都成70°的直线有    条？过大小为60°的二面角外一点P作与它的两个面都成60°的直线有    条？
    【答案】分析：根据异面直线a与b所成的角为60°，P为空间一点，过P分别作直线a，b的平行线，得到∠APB=60°，过P点作直线c，d分别是角∠APB的平分线和面APB的垂线，这时c与a，b所成角为30°，d与a，b所成角为90°，然后直线从c转到直线d的过程中一定经过30°、50°、60°、70°的角，可求出直线的条数．过大小为60°的二面角外一点P作与它的两个面都成60°的直线，可转化为过点P与两个平面的垂所成的角为30°，直线的条数．
    解答：解：把异面直线a，b平移到相交，使交点为P，
    此时∠APB=60°，过P点作直线c平分∠APB，这时c与a，b所成角为30°，一条
    过P点作直线d垂直a和b，这时d与a，b所成角为90°
    直线从c向两边转到d时与a，b所成角单调递增，必有经过30°、50°、60°、70°的角，
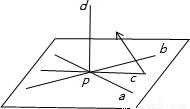
    因为两边，所以有2条．
    ∠AFE是度数为120°的二面角的一个平面角，AP是其的角平分线，当过点P的直线与AP平行时，满足条件，当过点P的直线与AD平行时，也满足条件，与AD类似，
    当过点P的直线与BE平行时，也满足条件，同理，在二面角为60°的两半平面内也存在两条直线满足条件．
    故答案为：1，2，3，4，5
    点评：此题是个中档题．考查异面直线所成的角，以及解决异面直线所成的角的方法（平移法）的应用，体现了转化的思想和运动变化的思想方法．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    5、已知异面直线a与b所成的角为50°，P为空间一点，则过点P与a、b所成的角都是300的直线有且仅有（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知两条异面直线a，b所成的角为
    π
    3
    ，直线l与a，直线l与b所成的角为θ，则θ的范围是（　　）
    A、[
    π
    6
    ，
    π
    2
    ]
    B、[
    π
    3
    ，
    π
    2
    ]
    C、[
    π
    6
    ，
    5π
    6
    ]
    D、[
    π
    3
    ，
    2π
    3
    ]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知：两条异面直线a、b所成的角为θ，它们的公垂线段AA1的长度为d．在直线a、b上分别取点E、F，设A1E=m，AF=n．求证：EF=
    		d2+m2+n2±2mncosθ
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2010•南充一模）已知两异面直线a，b所成的角为
    π
    3
    ，直线l分别与a，b所成的角都是θ，则θ的取值范围是
    [
    π
    6
    ，
    π
    2
    ]
    [
    π
    6
    ，
    π
    2
    ]
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设异面直线a、b所成的角为
    π
    3
    ，经过空间一点O有且只有一条直线l与异面直线a、b成等角θ，则θ的值为
    π
    6
    或
    π
    2
    π
    6
    或
    π
    2
    ．

    查看答案和解析>>

    同步练习册答案