
【题目】已知a>0且a≠1,函数f(x)=a ![]() 有最大值,则不等式loga(x2﹣5x+7)>0的解集为 .
有最大值,则不等式loga(x2﹣5x+7)>0的解集为 .
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设f(x)=|lgx|,且0<a<b<c时,有f(a)>f(c)>f(b),则( )
A.(a﹣1)(c﹣1)>0
B.ac>1
C.ac=1
D.ac<1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)为二次函数,﹣1和3是方程f(x)﹣x﹣4=0的两根,f(0)=1
(1)求f(x)的解析式;
(2)若在区间[﹣1,1]上,不等式f(x)>2x+m有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间生产某种产品,固定成本是![]() 万元,每生产
万元,每生产![]() 件产品成本增加
件产品成本增加![]() 元,根据经验,当年产量少于400件时,总收益
元,根据经验,当年产量少于400件时,总收益![]() (成本与总利润的和,单位:元)是年产量
(成本与总利润的和,单位:元)是年产量![]() (单位:件)的二次函数;,当年产量不少于
(单位:件)的二次函数;,当年产量不少于![]() 件时,R是Q的一次函数,以下是Q与R的部分数据:
件时,R是Q的一次函数,以下是Q与R的部分数据:
Q/ 件 | 50 | 200 | 350 | 500 | 650 |
R/ 元 | 23750 | 80000 | 113750 | 125000 | 1332500 |
问:每年生产多少件产品时,总利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家通过研究学生的学习行为发现;学生的接受能力与老师引入概念和描述问题所用的时间相关,教学开始时,学生的兴趣激增,学生的兴趣保持一段较理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用f(x)表示学生掌握和接受概念的能力,x表示讲授概念的时间(单位:min),可有以下的关系:f(x)= 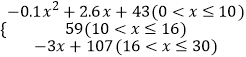
(Ⅰ)开讲后第5min与开讲后第20min比较,学生的接受能力何时更强一些?
(Ⅱ)开讲后多少min学生的接受能力最强?能维持多少时间?
(Ⅲ)若一个新数学概念需要55以上(包括55)的接受能力以及13min时间,那么老师能否在学生一直达到所需接受能力的状态下讲授完这个概念?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图). 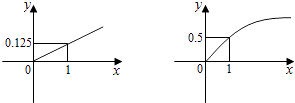
(1)分别写出两种产品的收益和投资的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎样分配资金能使投资获得最大的收益,其最大收益为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种大型商品,A,B两地都有出售,且价格相同、某地居民从两地之一购得商品后运回的费用是:每单位距离A地的运费是B地的运费的3倍,已知A,B两地距离为10千米,顾客选择A或B地购买这种商品的标准是:包括运费和价格的总费用较低,求A,B两地的售货区域的分界线的曲线形状,并指出曲线上、曲线内、曲线外的居民应如何选择购货地点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com