
【题目】已知三个关于x的不等式:①![]() ;②
;②![]() ;③
;③![]()
(1)分别求出①和②的解集;
(2)若同时满足①和②的x值也满足③,求m的取值范围;
(3)若同时满足③的x至少满足①和②的一个,求m的取值范围.
【答案】(1)①的解集为![]() ;②的解集为
;②的解集为![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由![]() 可知
可知![]() ,将此不等式与两边平方后的不等式联立
,将此不等式与两边平方后的不等式联立![]() ,解不等式组即可。(2)同时满足①和②的x值为
,解不等式组即可。(2)同时满足①和②的x值为![]() ,也满足③,进而由不等式
,也满足③,进而由不等式![]() 在
在![]() 时恒成立,求字母m的取值范围即可。(3)由同时满足③的x至少满足①和②的一个,可得不等式
时恒成立,求字母m的取值范围即可。(3)由同时满足③的x至少满足①和②的一个,可得不等式![]() 在
在![]() 或
或![]() 上恒成立,构造函数求字母m的取值范围即可。
上恒成立,构造函数求字母m的取值范围即可。
(1)不等式![]() 等价于
等价于![]() ,即
,即![]() ,所以
,所以![]() ,所以,不等式
,所以,不等式![]() 的解集为
的解集为![]() ;由
;由![]() 得
得![]() ,所以
,所以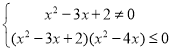 ,所以,
,所以,![]() 或
或![]() ,所以,不等式
,所以,不等式 ![]() 的解集为
的解集为![]() 。
。
(2)同时满足①和②的x值为![]() 。由同时满足①和②的x值也满足③,可得
。由同时满足①和②的x值也满足③,可得![]() 在
在![]() 时恒成立。令
时恒成立。令![]() ,因为
,因为![]() ,所以
,所以![]() ,解得
,解得![]() 。所以, m的取值范围为
。所以, m的取值范围为![]() 。
。
(3)令![]() ,由已知条件可得
,由已知条件可得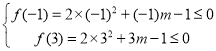 或
或![]() ,解得
,解得![]() ,所以,m的取值范围为
,所以,m的取值范围为![]() 。
。


科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对的边分别是a,b,c,向量![]() =(cos B,cos C),
=(cos B,cos C),![]() =(2a+c,b),且
=(2a+c,b),且![]() ⊥
⊥![]() .
.
(1)求角B的大小;
(2)若b=![]() ,求a+c的范围.
,求a+c的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地某高中2018年的高考考生人数是2015年高考考生人数的1.5倍.为了更好地对比该校考生的升学情况,统计了该校2015和2018年高考情况,得到如下饼图:

2018年与2015年比较,下列结论正确的是( )
A. 一本达线人数减少
B. 二本达线人数增加了0.5倍
C. 艺体达线人数相同
D. 不上线的人数有所增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图一是美丽的“勾股树”,它是一个直角三角形分别以它的每一边向外作正方形而得到.图二是第1代“勾股树”,重复图二的作法,得到图三为第2代“勾股树”,以此类推,已知最大的正方形面积为1,则第![]() 代“勾股树”所有正方形的个数与面积的和分别为( )
代“勾股树”所有正方形的个数与面积的和分别为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率低于![]() ,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着科学技术迅猛发展,国内有实力的企业纷纷进行海外布局,如在智能手机行业,国产品牌已在赶超国外巨头,某品牌手机公司一直默默拓展海外市场,在海外设多个分支机构需要国内公司外派大量80后、90后中青年员工.该企业为了解这两个年龄层员工对是否愿意接受外派工作的态度随机调查了100位员工,得到数据如下表:
愿意接受外派人数 | 不愿意接受外派人数 | 合计 | |
80后 | 20 | 20 | 40 |
90后 | 40 | 20 | 60 |
合计 | 60 | 40 | 100 |
(Ⅰ)根据调查的数据,判断能否在犯错误的概率不超过0.1的前提下认为“是否愿意接受外派与年龄层有关”,并说明理由;
(Ⅱ)该公司选派12人参观驻海外分支机构的交流体验活动,在参与调查的80后员工中用分层抽样方法抽出6名,组成80后组,在参与调查的90后员工中,也用分层抽样方法抽出6名,组成90后组
①求这12 人中,80后组90后组愿意接受外派的人数各有多少?
②为方便交流,在80后组、90后组中各选出3人进行交流,记在80后组中选到愿意接受外派的人数为![]() ,在90 后组中选到愿意接受外派的人数为
,在90 后组中选到愿意接受外派的人数为![]() ,求
,求![]() 的概率.
的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com