C
分析:A、B、C 共线,由
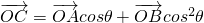
,得cosθ+(cosθ)
2=1,故(cosθ)
2=1-cosθ,cosθ=1-(cosθ)
2=(sinθ)
2,且(cosθ)
3=cosθ(cosθ)
2=2cosθ-1,所以sinθ+(sinθ)
2+(sinθ)
4+(sinθ)
6=sinθ+2cosθ.由此能求出sinθ+sin
2θ+sin
4θ+sin
6θ的最大值.
解答:∵A、B、C 共线,
∴由
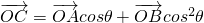
,
得 cosθ+(cosθ)
2=1,(三点共线的充要条件)
∴(cosθ)
2=1-cosθ,
cosθ=1-(cosθ)
2=(sinθ)
2,
且(cosθ)
3=cosθ(cosθ)
2=cosθ(1-cosθ)
=cosθ-(cosθ)
2=cosθ-(1-cosθ)
=2cosθ-1,
∴sinθ+(sinθ)
2+(sinθ)
4+(sinθ)
6=sinθ+cosθ+(cosθ)
2+(cosθ)
3=sinθ+cosθ+(1-cosθ)+(2cosθ-1)
=sinθ+2cosθ
因此,sinθ+sin
2θ+sin
4θ+sin
6θ的最大值=

=

.
故选C.
点评:本题考查平面向量的性质和应用,是基础题.解题时要认真审题,仔细解答,注意三角函数的性质的灵活运用.

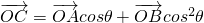 ,则sinθ+sin2θ+sin4θ+sin6θ的最大值是
,则sinθ+sin2θ+sin4θ+sin6θ的最大值是



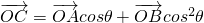 ,得cosθ+(cosθ)2=1,故(cosθ)2=1-cosθ,cosθ=1-(cosθ)2=(sinθ)2,且(cosθ)3=cosθ(cosθ)2=2cosθ-1,所以sinθ+(sinθ)2+(sinθ)4+(sinθ)6=sinθ+2cosθ.由此能求出sinθ+sin2θ+sin4θ+sin6θ的最大值.
,得cosθ+(cosθ)2=1,故(cosθ)2=1-cosθ,cosθ=1-(cosθ)2=(sinθ)2,且(cosθ)3=cosθ(cosθ)2=2cosθ-1,所以sinθ+(sinθ)2+(sinθ)4+(sinθ)6=sinθ+2cosθ.由此能求出sinθ+sin2θ+sin4θ+sin6θ的最大值.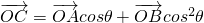 ,
, =
= .
.

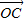 =cosθ
=cosθ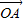 +cos2θ
+cos2θ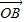 ,则sin2θ+sin4θ+sin6θ=( )
,则sin2θ+sin4θ+sin6θ=( )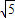
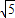
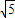 或1+
或1+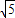
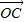 =cosθ
=cosθ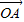 +cos2θ
+cos2θ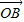 ,则sin2θ+sin4θ+sin6θ=( )
,则sin2θ+sin4θ+sin6θ=( )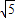
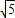
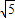 或1+
或1+