
【题目】如图,已知直三棱柱![]() 的底面是直角三角形,
的底面是直角三角形,![]() .
.

![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() 平面
平面![]() ;
;
![]() Ⅱ
Ⅱ![]() 求二面角
求二面角![]() 的余弦值;
的余弦值;
![]() Ⅲ
Ⅲ![]() 求点
求点![]() 到平面
到平面![]() 的距离.
的距离.
 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】某农科站技术员为了解某品种树苗的生长情况,在该批树苗中随机抽取一个容量为100的样本,测量树苗高度(单位:![]() ).经统计,高度在区间
).经统计,高度在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
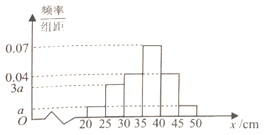
,![]() 分成6组,制成如图所示的频率分布直方图,其中高度不低于
分成6组,制成如图所示的频率分布直方图,其中高度不低于![]() 的树苗为优质树苗.
的树苗为优质树苗.
附:
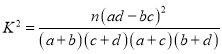 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
(1)求频率分布直方图中![]() 的值;
的值;
(2)已知所抽取的这100棵树苗来自于甲、乙两个地区,部分数据如下![]() 列联表所示,将列联表补充完整,并根据列联表判断是否有
列联表所示,将列联表补充完整,并根据列联表判断是否有![]() %的把握认为优质树苗与地区有关?
%的把握认为优质树苗与地区有关?
甲地区 | 乙地区 | 合计 | |
优质树苗 | 5 | ||
非优质树苗 | 25 | ||
合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次数学知识比赛中共有6个不同的题目,每位同学从中随机抽取3个题目进行作答,已知这6个题目中,甲只能正确作答其中的4个,而乙正确作答每个题目的概率均为![]() ,且甲、乙两位同学对每个题目的作答都是相互独立、互不影响的.
,且甲、乙两位同学对每个题目的作答都是相互独立、互不影响的.
(1)求甲、乙两位同学总共正确作答3个题目的概率;
(2)若甲、乙两位同学答对题目个数分别是![]() ,
,![]() ,由于甲所在班级少一名学生参赛,故甲答对一题得15分,乙答对一题得10分,求甲乙两人得分之和
,由于甲所在班级少一名学生参赛,故甲答对一题得15分,乙答对一题得10分,求甲乙两人得分之和![]() 的期望.
的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有橡皮泥制作的底面半径为5,高为9的圆锥和底面半径为![]() ,高为8的圆柱各一个.若将它们重新制作成总体积与各自的高均保持不变,但底面半径相同的新的圆锥与圆柱各一个,则新的底面半径为_________;若新圆锥的内接正三棱柱表面积取到最大值,则此正三棱柱的底面边长为_________.
,高为8的圆柱各一个.若将它们重新制作成总体积与各自的高均保持不变,但底面半径相同的新的圆锥与圆柱各一个,则新的底面半径为_________;若新圆锥的内接正三棱柱表面积取到最大值,则此正三棱柱的底面边长为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
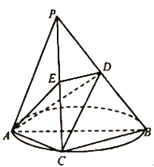
【题目】如图,![]() 是一个三棱锥,
是一个三棱锥,![]() 是圆的直径,
是圆的直径,![]() 是圆上的点,
是圆上的点,![]() 垂直圆所在的平面,
垂直圆所在的平面,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)若二面角![]() 是
是![]() ,
,![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点![]() 满足方程
满足方程![]() .
.
(1)求点M的轨迹C的方程;
(2)作曲线C关于![]() 轴对称的曲线,记为
轴对称的曲线,记为![]() ,在曲线C上任取一点
,在曲线C上任取一点![]() ,过点P作曲线C的切线l,若切线l与曲线
,过点P作曲线C的切线l,若切线l与曲线![]() 交于A,B两点,过点A,B分别作曲线
交于A,B两点,过点A,B分别作曲线![]() 的切线
的切线![]() ,证明
,证明![]() 的交点必在曲线C上.
的交点必在曲线C上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com