Question

类比在平面几何中关于角的命题“如果一个角的两条边与另一个角的两条边分别垂直，则这两个角相等或互补”，写出在空间中关于二面角相应的一个命题    ；
该命题是    命题（填“真”或“假”）．

Answer 1

【答案】分析：由平面图形中点的性质类比推理出空间里的线的性质，由平面图形中线的性质类比推理出空间中面的性质，由平面图形中面的性质类比推理出空间中体的性质．故由平面几何中的命题：“如果两个角的两边分别对应垂直，那么这两个角相等或互补”（边角的性质），我们可以推断在立体几何中，相关二面角和形成二面角的两个半平面的性质．
解答：解：在由平面图形的性质向空间物体的性质进行类比时，
我们常用由平面图形中线的性质类比推理出空间中面的性质，
故由平面几何中的命题：“如果两个角的两边分别对应垂直，那么这两个角相等或互补”（边角的性质），
我们可以推断在立体几何中：
“如果两个二面角的半平面分别对应垂直，那么这两个二面角角相等或互补”（面与二面角的性质）
但是这个命题不一定正确，如下图就是一个反例：

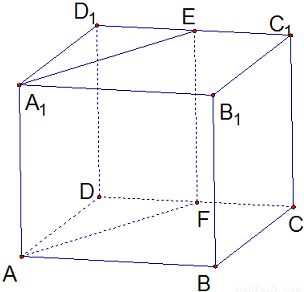
正方体ABCD-A₁B₁C₁D₁中，二面角D-AA₁-F与二面角D₁-DC-A的两个半平面就是分别对应垂直的，但是这两个二面角既不相等，也不互补．
答案为：“如果一个二面角的两个面与另一个二面角的两个面分别垂直，则这两个二面角相等或互补”，假．
点评：本题考查了几何中的类比推理问题，属于基础题．类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．