
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分为
分为![]() 、
、![]() 的中点,
的中点,![]() .
.
(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
(![]() )若
)若![]() ,求四面体
,求四面体![]() 的体积.
的体积.
(![]() )设
)设![]() ,若平面
,若平面![]() 与平面
与平面![]() 所成锐二面角
所成锐二面角![]() ,求
,求![]() 的取值范围.
的取值范围.

【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由题目给出的条件,可得四边形ABFD为矩形,说明AB⊥BF,再证明AB⊥EF,由线面垂直的判定可得AB⊥面BEF,再根据面面垂直的判定得到平面ABE⊥平面BEF;
(2)明确锥体的高为![]() ,即可得到几何体的体积;
,即可得到几何体的体积;
(3)以A点为坐标原点,AB、AD、AP所在直线分别为x、y、z轴建立空间坐标系,利用平面法向量所成交与二面角的关系求出二面角的余弦值,根据给出的二面角的范围得其余弦值的范围,最后求解不等式可得a的取值范围.

(![]() )证明:∵
)证明:∵![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,
∴![]() 为矩形,
为矩形,![]() ,
,
又∵![]() ,
,![]() 是
是![]() 中点,
中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(![]() )∵
)∵![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() ,
,
∴![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() 的面积
的面积![]() ,
,
∴四面体![]() 的体积
的体积![]() .
.
(![]() )∵
)∵![]() ,
,
∴![]() ,
,
又![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
如图,以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
平面![]() 的法向量
的法向量![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则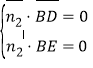 ,即
,即 ,取
,取![]() ,得
,得![]() ,
,![]() ,
,
则![]() ,
,
∴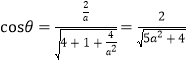 ,
,
∵平面![]() 与平面
与平面![]() 所成锐二面角
所成锐二面角![]() ,
,
∴![]() ,即
,即![]() ,
,
由![]() ,得:
,得:![]() ,由
,由![]() 得:
得:![]() 或
或![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,已知平面ADC∥平面A1B1C1 , B为线段AD的中点,△ABC≈△A1B1C1 , 四边形ABB1A1为正方形,平面AA1C1C丄平面ADB1A1 , A1C1=A1A,∠C1A1A= ![]() ,M为棱A1C1的中点.
,M为棱A1C1的中点.
(Ⅰ)若N为线段DC1上的点,且直线MN∥平面ADB1A1 , 试确定点N的位置;
(Ⅱ)求平面MAD与平面CC1D所成的锐二面角的余弦值.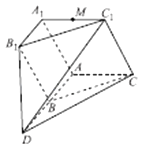
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,直线l:y=x+2与以原点为圆心、椭圆C的短半轴为半径的圆O相切.
,直线l:y=x+2与以原点为圆心、椭圆C的短半轴为半径的圆O相切.
(1)求椭圆C的方程;
(2)过椭圆C的左顶点A作直线m,与圆O相交于两点R,S,若△ORS是钝角三角形,求直线m的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用半径为R的圆铁皮剪一个内接矩形,再以内接矩形的两边分别作为圆柱的高与底面半径,则圆柱的体积最大时,该圆铁皮面积与其内接矩形的面积比为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABC﹣A1B1C1中,CC1⊥平面ABC,AB=2A1B1=2CC1 , M,N分别为AC,BC的中点. 
(1)求证:AB1∥平面C1MN;
(2)若AB⊥BC且AB=BC,求二面角C﹣MC1﹣N的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过点C,已知AB=2米,AD=1米.

(1)要使矩形AMPN的面积大于9平方米,则DN的长应在什么范围内?
(2)当DN的长度为多少时,矩形花坛AMPN的面积最小?并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某省各景区在大众中的熟知度,随机从本省![]() 岁的人群中抽取了
岁的人群中抽取了![]() 人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该省有哪几个国家
人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该省有哪几个国家![]() 级旅游景区?”,统计结果如下表所示:
级旅游景区?”,统计结果如下表所示:
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
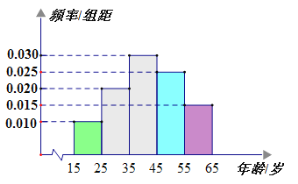
(1)分别求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组抽取的人数;
组每组抽取的人数;
(3)在(2)中抽取的![]() 人中随机抽取
人中随机抽取![]() 人,求所抽取的人中恰好没有年龄段在
人,求所抽取的人中恰好没有年龄段在![]() 的概率
的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com