
| A. | $\frac{π}{8}$ | B. | $\frac{π}{8}+\frac{1}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{4}+\frac{1}{4}$ |
分析 求得正方形的面积,则S(M)=S△DGH+S△AEH+S扇形EGH,根据几何概率概率公式可知:P(M)=$\frac{S(M)}{{S}_{ABCD}}$,即可求得满足|PH|<$\sqrt{2}$的概率.
解答 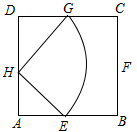 解:(1)如图所示,正方形的面积S正方形ABCD=2×2=4.
解:(1)如图所示,正方形的面积S正方形ABCD=2×2=4.
设“满足|PH|>$\sqrt{2}$的正方形内部的点P的集合”为事件M,
则S(M)=S△DGH+S△AEH+S扇形EGH=2×$\frac{1}{2}$×1×1+$\frac{1}{2}$×$\sqrt{2}$×$\frac{π}{2}$×$\sqrt{2}$=1+$\frac{π}{2}$,
∴P(M)=$\frac{1+\frac{π}{2}}{4}$=$\frac{π}{8}$+$\frac{1}{4}$.
故满足|PH|<$\sqrt{2}$的概率为$\frac{π}{8}$+$\frac{1}{4}$.
故选B.
点评 本题考查几何概率概率公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ | B. | $({-\frac{{\sqrt{3}}}{3},0})∪({0,\frac{{\sqrt{3}}}{3}})$ | C. | $[{-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}}]$ | D. | $({-∞,-\frac{{\sqrt{3}}}{3}})∪({\frac{{\sqrt{3}}}{3},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
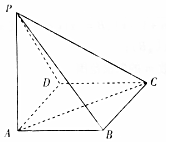 如图,在底面为正方形的四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA⊥AD,PA=AD,则异面直线PB与AC所成的角为( )
如图,在底面为正方形的四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA⊥AD,PA=AD,则异面直线PB与AC所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 672 | B. | 673 | C. | 3024 | D. | 1345 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com