
【题目】已知椭圆C:![]() =1(a>b>0),点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:x2+y2=
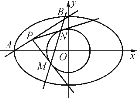
=1(a>b>0),点A、B分别是椭圆C的左顶点和上顶点,直线AB与圆G:x2+y2=![]() (c是椭圆的半焦距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
(c是椭圆的半焦距)相离,P是直线AB上一动点,过点P作圆G的两切线,切点分别为M、N.
(1)若椭圆C经过两点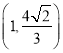 、
、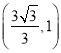 ,求椭圆C的方程;
,求椭圆C的方程;
(2)当c为定值时,求证:直线MN经过一定点E,并求![]() ·
·![]() 的值(O是坐标原点);
的值(O是坐标原点);
(3)若存在点P使得△PMN为正三角形,试求椭圆离心率的取值范围..
【答案】(1)![]() =1.(2)见解析(3)
=1.(2)见解析(3)![]()
【解析】(1)解:令椭圆mx2+ny2=1,其中m=![]() ,n=
,n=![]() ,得
,得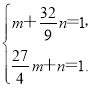 所以m=
所以m=![]() ,n=
,n=![]() ,即椭圆方程为
,即椭圆方程为![]() =1.
=1.
(2)证明:直线AB:![]() =1,设点P(x0,y0),则OP的中点为
=1,设点P(x0,y0),则OP的中点为![]() ,所以点O、M、P、N所在的圆的方程为
,所以点O、M、P、N所在的圆的方程为![]() =
=![]() ,化简为x2-x0x+y2-y0y=0,与圆x2+y2=
,化简为x2-x0x+y2-y0y=0,与圆x2+y2=![]() 作差,即直线MN:x0x+y0y=
作差,即直线MN:x0x+y0y=![]() .
.
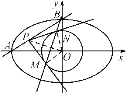
因为点P(x0,y0)在直线AB上,得![]() =1,
=1,
所以x0 ![]() +
+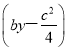 =0,即
=0,即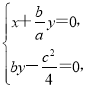
得x=-![]() ,y=
,y=![]() ,故定点E
,故定点E 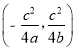 ,
,![]() ·
·![]() =
=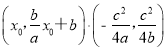 =
=![]() .
.
(3)解:由直线AB与圆G:x2+y2=![]() (c是椭圆的焦半距)相离,则
(c是椭圆的焦半距)相离,则![]() >
>![]() ,即4a2b2>c2(a2+b2),4a2(a2-c2)>c2(2a2-c2),得e4-6e2+4>0.因为0<e<1,所以0<e2<3-
,即4a2b2>c2(a2+b2),4a2(a2-c2)>c2(2a2-c2),得e4-6e2+4>0.因为0<e<1,所以0<e2<3-![]() ①.连结ON、OM、OP,若存在点P使△PMN为正三角形,则在Rt△OPN中,OP=2ON=2r=c,所以
①.连结ON、OM、OP,若存在点P使△PMN为正三角形,则在Rt△OPN中,OP=2ON=2r=c,所以![]() ≤c,a2b2≤c2(a2+b2),a2(a2-c2)≤c2(2a2-c2),得e4-3e2+1≤0.因为0<e<1,所以
≤c,a2b2≤c2(a2+b2),a2(a2-c2)≤c2(2a2-c2),得e4-3e2+1≤0.因为0<e<1,所以![]() ≤e2<1,②.由①②得
≤e2<1,②.由①②得![]() ≤e2<3-
≤e2<3-![]() ,所以
,所以![]()


科目:高中数学 来源: 题型:
【题目】对于数列![]() ,定义
,定义![]() ,
, ![]() .
.
(1) 若![]() ,是否存在
,是否存在![]() ,使得
,使得![]() ?请说明理由;
?请说明理由;
(2) 若![]() ,
, ![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3) 令![]() ,求证:“
,求证:“![]() 为等差数列”的充要条件是“
为等差数列”的充要条件是“![]() 的前4项为等差数列,且
的前4项为等差数列,且![]() 为等差数列”.
为等差数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆方程为![]() .
.
(1)设椭圆的左右焦点分别为![]() 、
、![]() ,点
,点![]() 在椭圆上运动,求
在椭圆上运动,求![]() 的值;
的值;
(2)设直线![]() 和圆
和圆![]() 相切,和椭圆交于
相切,和椭圆交于![]() 、
、![]() 两点,
两点,![]() 为原点,线段
为原点,线段![]() 、
、![]() 分别和圆
分别和圆![]() 交于
交于![]() 、
、![]() 两点,设
两点,设![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 共有
共有![]() 项,记该数列前
项,记该数列前![]() 项
项![]() 中的最大项为
中的最大项为![]() ,该数列后
,该数列后![]() 项
项![]() 中的最小项为
中的最小项为![]() ,
,![]() .
.
(1)若数列![]() 的通项公式为
的通项公式为![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)试构造一个数列![]() ,满足
,满足![]() ,其中
,其中![]() 是公差不为零的等差数列,
是公差不为零的等差数列,![]() 是等比数列,使得对于任意给定的正整数
是等比数列,使得对于任意给定的正整数![]() ,数列
,数列![]() 都是单调递增的,并说明理由.
都是单调递增的,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
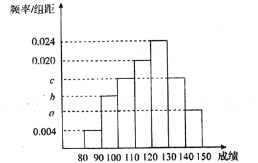
【题目】高三年级某班50名学生期中考试数学成绩的频率分布直方图如图所示,成绩分组区间为:![]()
![]()
![]()
![]()
![]()
![]()
![]() .其中a,b,c成等差数列且
.其中a,b,c成等差数列且![]() .物理成绩统计如表.(说明:数学满分150分,物理满分100分)
.物理成绩统计如表.(说明:数学满分150分,物理满分100分)
分组 |
|
|
|
|
|
频数 | 6 | 9 | 20 | 10 | 5 |
(1)根据频率分布直方图,请估计数学成绩的平均分;
(2)根据物理成绩统计表,请估计物理成绩的中位数;
(3)若数学成绩不低于140分的为“优”,物理成绩不低于90分的为“优”,已知本班中至少有一个“优”同学总数为6人,从数学成绩为“优”的同学中随机抽取2人,求两人恰好均为物理成绩“优”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]() ,且P到抛物线焦点的距离为2直线
,且P到抛物线焦点的距离为2直线![]() 过点
过点![]() ,且与抛物线相交于A,B两点.
,且与抛物线相交于A,B两点.
(Ⅰ)求抛物线的方程;
(Ⅱ)若点Q恰为线段AB的中点,求直线![]() 的方程;
的方程;
(Ⅲ)过点![]() 作直线MA,MB分别交抛物线于C,D两点,请问C,D,Q三点能否共线?若能,求出直线
作直线MA,MB分别交抛物线于C,D两点,请问C,D,Q三点能否共线?若能,求出直线![]() 的斜率
的斜率![]() ;若不能,请说明理由.
;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解高一年级学生学习数学的状态,从期中考试成绩中随机抽取50名学生的数学成绩,按成绩分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
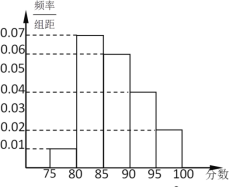
(1)由频率分布直方图,估计这50名学生数学成绩的中位数和平均数(保留到0.01);
(2)该校高一年级共有1000名学生,若本次考试成绩90分以上(含90分)为“优秀”等次,则根据频率分布直方图估计该校高一学生数学成绩达到“优秀”等次的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行六面体ABCD﹣A1B1C1D1中,AA1=A1D,AB=BC,∠ABC=120°.
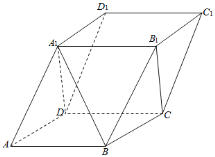
(1)证明:AD⊥BA1;
(2)若平面ADD1A1⊥平面ABCD,且A1D=AB,求直线BA1与平面A1B1CD所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com