分析:(Ⅰ)过P点作PM⊥AB于M,由正三棱柱性质知PM⊥平面ABC,过M作MN⊥AC于N,连接PN,则PN⊥AC,从而∠PNM为二面角P-AC-B的平面角,在Rt△PMN中,可求二面角P-AC-B的正切值.
(Ⅱ)根据M是AB中点,可知B到平面PAC距离等于M到平面PAC距离的2倍,过M作MQ⊥PN于Q,则MQ⊥平面PAC,可求M到平面PAC距离,从而可求点B到平面PAC距离.
解答:
解:(Ⅰ)过P点作PM⊥AB于M,由正三棱柱性质知PM⊥平面ABC,
连接MC,则MC为PC在平面ABC上的射影.
∵PC⊥AB,∴MC⊥AB,∴M为AB中点,
又PM∥AA
1,所以P为A
1B的中点.
过M作MN⊥AC于N,连接PN,则PN⊥AC,∴∠PNM为二面角P-AC-B的平面角
在Rt△PMN中,由|PM|=
,
|MN|=a,得
tan∠PNM==.
所以二面角P-AC-B的正切值为
…(6分)
(Ⅱ)∵M是AB中点,∴B到平面PAC距离等于M到平面PAC距离的2倍,
又由(I)知AC⊥平面PMN,∴平面PMN⊥平面PAC,
过M作MQ⊥PN于Q,则MQ⊥平面PAC,
|MQ|===a.
故所求点B到平面PAC距离为
a…(12分)
点评:本题以正三棱柱为载体,考查面面角,考查点到面的距离,关键是作出面面角,寻找表示点面距离的线段.

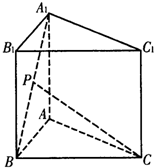 已知正三棱柱ABC-A1B1C的各条棱长都为a,P为A1B上的点,且PC⊥AB
已知正三棱柱ABC-A1B1C的各条棱长都为a,P为A1B上的点,且PC⊥AB 解:(Ⅰ)过P点作PM⊥AB于M,由正三棱柱性质知PM⊥平面ABC,
解:(Ⅰ)过P点作PM⊥AB于M,由正三棱柱性质知PM⊥平面ABC,

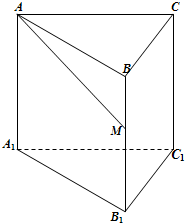 如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ. 已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.
已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.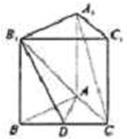 如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1. (2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.
(2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.