练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知△ABC的三个顶点的坐标为A（0，1），B（1，0），C（0，﹣2），O为坐标原点，动点M满足| |=1，则| + + |的最大值是（ ）
    A.
    B.
    C. ﹣1
    D. ﹣1

    【答案】A
    【解析】解：设点M的坐标是（x，y）， ∵C（0，﹣2），且| |=1，
    ∴ ，则x2+（y+2）2=1，
    即动点M的轨迹是以C为圆心、1为半径的圆，
    ∵A（0，1），B（1，0），
    ∴ + + =（x+1，y+1），
    则| + + |= ，几何意义表示：
    点M（x，y）与点A（﹣1，﹣1）之间的距离，即圆C上的点与点A（﹣1，﹣1）的距离，
    ∵点A（﹣1，﹣1）在圆C外部，
    ∴| + + |的最大值是|AC|+1= +1= ，
    故选A．
    【考点精析】掌握平面向量的坐标运算是解答本题的根本，需要知道坐标运算：设，则;;设，则．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设△AnBnCn的三边长分别为an ， bn ， cn ， n=1，2，3…，若b1＞c1 ， b1+c1=2a1 ， an+1=an ， bn+1= ，cn+1= ，则∠An的最大值是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某重点中学为了解高一年级学生身体发育情况，对全校700名高一年级学生按性别进行分层抽样检查，测得身高（单位：cm）频数分布表如表1、表2． 表1：男生身高频数分布表

    身高（cm）

    [160，165）

    [165，170）

    [170，175）

    [175，180）

    [180，185）

    [185，190）

    频数

    2

    5

    14

    13

    4

    2

    表2：女生身高频数分布表

    身高（cm）

    [150，155）

    [155，160）

    [160，165）

    [165，170）

    [170，175）

    [175，180）

    频数

    1

    7

    12

    6

    3

    1


    （1）求该校高一女生的人数；
    （2）估计该校学生身高在[165，180）的概率；
    （3）以样本频率为概率，现从高一年级的男生和女生中分别选出1人，设X表示身高在[165，180）学生的人数，求X的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|x﹣a|，若不等式f（x）≤3的解集为{|x|﹣1≤x≤5}． （Ⅰ）求实数a的值：
    （Ⅱ）若不等式f（3x）+f（x+3）≥m对一切实数x恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ax+lnx，其中a为常数，设e为自然对数的底数．
    （1）当a=﹣1时，求f（x）的最大值；
    （2）若f（x）在区间（0，e]上的最大值为﹣3，求a的值；
    （3）设g（x）=xf（x），若a＞0，对于任意的两个正实数x1 ， x2（x1≠x2），证明：2g（ ）＜g（x1）+g（x2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某品牌的汽车4S店，对最近100例分期付款购车情况进行统计，统计结果如表所示，已知分9期付款的频率为0.4；该店经销一辆该品牌的汽车．若顾客分3期付款，其利润为1万元；分6期或9期付款，其利润为2万元；分12期付款，其利润为3万元．

    付款方式

    分3期

    分6期

    分9期

    分12期

    频数

    20

    20

    a

    b


    （1）若以表中计算出的频率近似替代概率，从该店采用分期付款购车的顾客（数量较大）中随机抽取3位顾客，求事件A：“至多有1位采用分6期付款”的概率P（A）；
    （2）按分层抽样的方式从这100位顾客中抽出5人，再从抽出的5人中随机抽取3人，记该店在这3人身上赚取的总利润为随机变量η，求η的分布列及数学期望E（η）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入a，b的值分别是21，28，则输出a的值为（ ）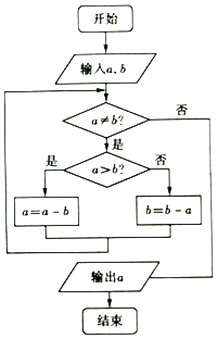
    A.14
    B.7
    C.1
    D.0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在数列{an}和{bn}中，a1= ，{an}的前n项为Sn ， 满足Sn+1+（ ）n+1=Sn+（ ）n（n∈N*），bn=（2n+1）an ， {bn}的前n项和为Tn ．
    （1）求数列{bn}的通项公式bn以及Tn ．
    （2）若T1+T3 ， mT2 ， 3（T2+T3）成等差数列，求实数m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在（0，+∞）上的函数f（x）满足f′（x）+2f（x）= ，且f（1）= ，则不等式f（lnx）＞f（3）的解集为（ ）
    A.（﹣∞，e3）
    B.（0，e3）
    C.（1，e3）
    D.（e3 ， +∞）

    查看答案和解析>>

    同步练习册答案