
【题目】如图,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
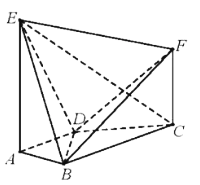
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)若二面角![]() 的余弦值为
的余弦值为![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(Ⅰ)见证明;(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
首先利用几何体的特征建立空间直角坐标系
(Ⅰ)利用直线BF的方向向量和平面ADE的法向量的关系即可证明线面平行;
(Ⅱ)分别求得直线CE的方向向量和平面BDE的法向量,然后求解线面角的正弦值即可;
(Ⅲ)首先确定两个半平面的法向量,然后利用二面角的余弦值计算公式得到关于CF长度的方程,解方程可得CF的长度.
依题意,可以建立以A为原点,分别以![]() 的方向为x轴,y轴,z轴正方向的空间直角坐标系(如图),
的方向为x轴,y轴,z轴正方向的空间直角坐标系(如图),
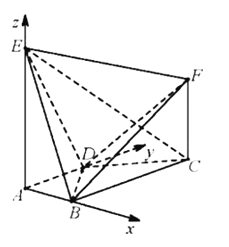
可得![]() .
.
设![]() ,则
,则![]() .
.
(Ⅰ)依题意,![]() 是平面ADE的法向量,
是平面ADE的法向量,
又![]() ,可得
,可得![]() ,
,
又因为直线![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)依题意,![]() ,
,
设![]() 为平面BDE的法向量,
为平面BDE的法向量,
则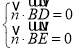 ,即
,即![]() ,
,
不妨令z=1,可得![]() ,
,
因此有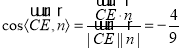 .
.
所以,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(Ⅲ)设![]() 为平面BDF的法向量,则
为平面BDF的法向量,则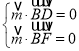 ,即
,即![]() .
.
不妨令y=1,可得![]() .
.
由题意,有 ,解得
,解得![]() .
.
经检验,符合题意
所以,线段![]() 的长为
的长为![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】下面使用类比推理正确的是( )
A. 直线a∥b,b∥c,则a∥c,类推出:向量![]() ,则
,则![]()
B. 同一平面内,直线a,b,c,若a⊥c,b⊥c,则a∥b.类推出:空间中,直线a,b,c,若a⊥c,b⊥c,则a∥b
C. 实数a,b,若方程x2+ax+b=0有实数根,则a2≥4b.类推出:复数a,b,若方程x2+ax+b=0有实数根,则a2≥4b
D. 以点(0,0)为圆心,r为半径的圆的方程为x2+y2=r2.类推出:以点(0,0,0)为球心,r为半径的球的方程为x2+y2+z2=r2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线l:x﹣y+4=0和圆O:x2+y2=4,P是直线l上一点,过点P作圆C的两条切线,切点分别为M,N.
(1)若PM⊥PN,求点P坐标;
(2)若圆O上存在点A,B,使得∠APB=60°,求点P的横坐标的取值范围;
(3)设线段MN的中点为Q,l与x轴的交点为T,求线段TQ长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学习小组通过对某商场一种品牌服装销售情况的调查发现:该服装在过去的一个月内(以![]() 天计),日销售量
天计),日销售量 ![]() (件)与时间x (天)的部分数据如下表所示,给出以下四种函数模型:①
(件)与时间x (天)的部分数据如下表所示,给出以下四种函数模型:① ![]() ,②
,② ![]() ,③
,③ ![]() ④
④![]() .请你根据上表中的数据,从中选择你认为最合适的一种函数来描述日销售量
.请你根据上表中的数据,从中选择你认为最合适的一种函数来描述日销售量![]() (件)与时间x(天)的变化关系,请将你选择的函数序号填写在横线上__________.(不需要求出具体解析式)
(件)与时间x(天)的变化关系,请将你选择的函数序号填写在横线上__________.(不需要求出具体解析式)
x (天) | 10 | 20 | 25 | 30 |
| 110 | 120 | 125 | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列说法正确的是( )
A.若m∥α,n∥α,则 m∥n
B.若α⊥γ,β⊥γ,则α∥β
C.若m⊥α,n⊥β,且α⊥β,则m⊥n.
D.若m∥α,n∥α,且mβ, nβ,则α∥β
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com