
【题目】椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,椭圆上一点
,椭圆上一点![]() 与
与![]() ,
,![]() 的距离之和为
的距离之和为![]() ,且焦距是短轴长的2倍.
,且焦距是短轴长的2倍.
(1)求椭圆的方程;
(2)过线段![]() 上一点的直线
上一点的直线![]() (斜率不为0)与椭圆相交于
(斜率不为0)与椭圆相交于![]() ,
,![]() 两点,当
两点,当![]() 的面积与
的面积与![]() 的面积之比为
的面积之比为![]() 时,求
时,求![]() 面积的最大值.
面积的最大值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】将一枚棋子放在一个![]() 的棋盘上,记
的棋盘上,记![]() 为从左、上数第
为从左、上数第![]() 行第
行第![]() 列的小方格,求所有的四元数组
列的小方格,求所有的四元数组![]() ,使得从
,使得从![]() 出发,经过每个小方格恰一次到达
出发,经过每个小方格恰一次到达![]() (每步为将棋子从一个小方格移到与之有共同边的另一个小方格).
(每步为将棋子从一个小方格移到与之有共同边的另一个小方格).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题![]() 方程
方程![]() 表示双曲线;命题
表示双曲线;命题![]() 不等式
不等式![]() 的解集是
的解集是![]() .
. ![]() 为假,
为假, ![]() 为真,求
为真,求![]() 的取值范围.
的取值范围.
【答案】![]()
【解析】试题分析:由命题![]() 方程
方程![]() 表示双曲线,求出
表示双曲线,求出![]() 的取值范围,由命题
的取值范围,由命题![]() 不等式
不等式![]() 的解集是
的解集是![]() ,求出
,求出![]() 的取值范围,由
的取值范围,由![]() 为假,
为假, ![]() 为真,得出
为真,得出![]() 一真一假,分两种情况即可得出
一真一假,分两种情况即可得出![]() 的取值范围.
的取值范围.
试题解析:
![]() 真
真 ![]()
![]() ,
,
![]() 真
真 ![]() 或
或![]()
![]()
∴![]()
![]() 真
真![]() 假
假 ![]()
![]() 假
假![]() 真
真 ![]()
∴![]() 范围为
范围为![]()
【题型】解答题
【结束】
18
【题目】如图,设![]() 是圆
是圆![]() 上的动点,点
上的动点,点![]() 是
是![]() 在
在![]() 轴上的投影,
轴上的投影, ![]() 为
为![]() 上一点,且
上一点,且![]() .
.
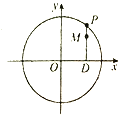
(1)当![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)求过点![]() 且斜率为
且斜率为![]() 的直线被
的直线被![]() 所截线段的长度.
所截线段的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个三角形的边长与面积都是整数,则称为“海伦三角形”;三边长互质的海伦三角形,称为“本原海伦三角形”;边长都不是3的倍数的本原海伦三角形,称为“奇异三角形”.
(1)求奇异三角形的最小边长的最小值;
(2)求证:等腰的奇异三角形有无数个;
(3)问:非等腰的奇异三角形有多少个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球运动员的投篮命中率为![]() ,他想提高自己的投篮水平,制定了一个夏季训练计划
,他想提高自己的投篮水平,制定了一个夏季训练计划![]() 为了了解训练效果,执行训练前,他统计了10场比赛的得分,计算出得分的中位数为15分,平均得分为15分,得分的方差为
为了了解训练效果,执行训练前,他统计了10场比赛的得分,计算出得分的中位数为15分,平均得分为15分,得分的方差为![]() 执行训练后也统计了10场比赛的得分,成绩茎叶图如图所示:
执行训练后也统计了10场比赛的得分,成绩茎叶图如图所示:

![]() 请计算该篮球运动员执行训练后统计的10场比赛得分的中位数、平均得分与方差;
请计算该篮球运动员执行训练后统计的10场比赛得分的中位数、平均得分与方差;
![]() 如果仅从执行训练前后统计的各10场比赛得分数据分析,你认为训练计划对该运动员的投篮水平的提高是否有帮助?为什么?
如果仅从执行训练前后统计的各10场比赛得分数据分析,你认为训练计划对该运动员的投篮水平的提高是否有帮助?为什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设某市2011年新建住房400万m2,其中250万m2是中低价房,预计在今后的若干年内,该市每年新建住房面积平均比上一年增长8%.另外,每年新建住房中,中低价房的面积比上一年增加50万m2,那么到哪一年底,
(1)该市历年所建中低价房的累计面积(以2011年为累计的第一年)将首次不少于4750万m2?
(2)当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com