
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,设
时,设![]() ,求
,求![]() 在区间
在区间![]() 上的最大值.
上的最大值.
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为
的长轴长为![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆![]() 的左焦点为
的左焦点为![]() ,点
,点![]() 是椭圆与
是椭圆与![]() 轴负半轴的交点,经过
轴负半轴的交点,经过![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() ,经过
,经过![]() 且与
且与![]() 平行的直线与椭圆交于点
平行的直线与椭圆交于点![]() ,若
,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出![]() 吨该商品可获利润
吨该商品可获利润![]() 万元,未售出的商品,每
万元,未售出的商品,每![]() 吨亏损
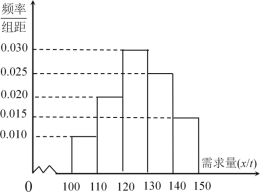
吨亏损![]() 万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了
万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了![]() 吨该商品.现以
吨该商品.现以![]() (单位:吨,
(单位:吨,![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量,![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(1)将![]() 表示为
表示为![]() 的函数,求出该函数表达式;
的函数,求出该函数表达式;
(2)根据直方图估计利润![]() 不少于57万元的概率;
不少于57万元的概率;
(3)根据频率分布直方图,估计一个销售季度内市场需求量![]() 的平均数与中位数的大小(保留到小数点后一位).
的平均数与中位数的大小(保留到小数点后一位).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),将曲线
为参数),将曲线![]() 上各点的横坐标都缩短为原来的
上各点的横坐标都缩短为原来的![]() 倍,纵坐标坐标都伸长为原来的
倍,纵坐标坐标都伸长为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,在极坐标系(与直角坐标系
,在极坐标系(与直角坐标系![]() 取相同的单位长度,且以原点
取相同的单位长度,且以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标![]() 中,圆
中,圆![]() ,圆
,圆![]() 。
。
(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆![]() 的极坐标方程,并求出圆
的极坐标方程,并求出圆![]() 的交点坐标(用极坐标表示);
的交点坐标(用极坐标表示);
(Ⅱ)求圆![]() 的公共弦的参数方程。
的公共弦的参数方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像是由函数
的图像是由函数![]() 的图像经如下变换得到:先将
的图像经如下变换得到:先将![]() 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移
图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移![]() 个单位长度.
个单位长度.
(Ⅰ)求函数![]() 的解析式,并求其图像的对称轴方程;
的解析式,并求其图像的对称轴方程;
(Ⅱ)已知关于![]() 的方程
的方程![]() 在
在![]() 内有两个不同的解
内有两个不同的解![]() .
.
(1)求实数m的取值范围;
(2)证明:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙二人进行一次象棋比赛,每局胜者得1分,负者得0分(无平局),约定一方得4分时就获得本次比赛的胜利并且比赛结束,设在每局比赛中,甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,各局比赛结果相互独立,已知前3局中,甲得1分,乙得2分.
,各局比赛结果相互独立,已知前3局中,甲得1分,乙得2分.
(1)求甲获得这次比赛胜利的概率;
(2)设![]() 表示从第4局开始到比赛结束所进行的局数,求
表示从第4局开始到比赛结束所进行的局数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于命题的说法错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B.“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
C.“若![]() 为
为![]() 的极值点,则
的极值点,则![]() ”的逆命题为真
”的逆命题为真
D.命题![]() :
:![]() ,
,![]() 的否定是
的否定是![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com