
【题目】如图,圆台的上、下底面半径分别为5cm,10cm,母线长![]() ,从圆台母线
,从圆台母线![]() 的中点
的中点![]() 拉一条绳子绕圆台侧面转到
拉一条绳子绕圆台侧面转到![]() 点.求:
点.求:

(1)绳子的最短长度;
(2)在绳子最短时,求上底面圆周上的点到绳子的最短距离.
【答案】(1)50cm;(2)4cm
【解析】
(1)根据题意,将圆台展开成平面图形,由两点间距离最短可得绳子![]() 即为所求的线段长.由圆台上下底面的半径,结合相似即可求得
即为所求的线段长.由圆台上下底面的半径,结合相似即可求得![]() 的长.根据弧长、圆心角、半径关系,可在扇形
的长.根据弧长、圆心角、半径关系,可在扇形![]() 中求得圆心角.进而由勾股定理求得最短距离
中求得圆心角.进而由勾股定理求得最短距离![]() 的长度.
的长度.
(2)过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() 的长度为所求最短距离.利用等面积法可求得
的长度为所求最短距离.利用等面积法可求得![]() ,进而求得
,进而求得![]() 的长度.
的长度.
(1)如图,绳子的最短长度为侧面展开图中![]() 的长度.
的长度.

因为圆台的上、下底面半径分别为5cm,10cm
所以![]() ,
,
母线长![]() ,代入可得
,代入可得![]() ,
,
所以![]() .
.
设![]() ,由
,由![]() ,
,
解得![]() .
.
所以![]() .
.
即绳子的最短长度为50cm.
(2)过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() 的长度为所求最短距离.
的长度为所求最短距离.
因为![]() ,
,
所以![]() .
.
故![]() ,即上底面圆周上的点到绳子的最短距离为4cm.
,即上底面圆周上的点到绳子的最短距离为4cm.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某小型企业甲产品生产的投入成本x(单位:万元)与产品销售收入y(单位:万元)存在较好的线性关系,下表记录了最近5次该产品的相关数据.
x(万元) | 3 | 5 | 7 | 9 | 11 |
y(万元) | 8 | 10 | 13 | 17 | 22 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本12万元的毛利率更大还是投入成本15万元的毛利率更大(毛利率![]()
![]()
![]() )?
)?
相关公式: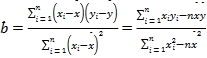 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,底面是边长为4的正三角形,
中,底面是边长为4的正三角形,![]() ,
,![]() 底面
底面![]() ,点
,点![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)当![]() 时,函数
时,函数![]() 有两个极值点,求
有两个极值点,求![]() 的取值范围;
的取值范围;
(2)若![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,且函数
轴平行,且函数![]() 在
在![]() 时,其图象上每一点处切线的倾斜角均为锐角,求
时,其图象上每一点处切线的倾斜角均为锐角,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列![]() 个结论:
个结论:
①棱长均相等的棱锥一定不是六棱锥;
②函数![]() 既不是奇函数又不是偶函数;
既不是奇函数又不是偶函数;
③若函数![]() 的值域为
的值域为![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() ;
;
④若函数![]() 满足条件
满足条件![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
其中正确的结论的序号是:______. (写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中在校学生2000人![]() 为了响应“阳光体育运动”号召,学校举行了跑步和登山比赛活动
为了响应“阳光体育运动”号召,学校举行了跑步和登山比赛活动![]() 每人都参加而且只参与了其中一项比赛,各年级参与比赛人数情况如表:
每人都参加而且只参与了其中一项比赛,各年级参与比赛人数情况如表:
高一年级 | 高二年级 | 高三年级 | |
跑步 | a | b | c |
登山 | x | y | z |
其中a:b:![]() :3:5,全校参与登山的人数占总人数的
:3:5,全校参与登山的人数占总人数的![]() ,为了了解学生对本次活动的满意程度,现用分层抽样方式从中抽取一个100个人的样本进行调查,则高二年级参与跑步的学生中应抽取
,为了了解学生对本次活动的满意程度,现用分层抽样方式从中抽取一个100个人的样本进行调查,则高二年级参与跑步的学生中应抽取![]()
![]()
A. 6人B. 12人C. 18人D. 24人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com