练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数的一个零点为-2，当时最大值为0．

    （1）求的值；

    （2）若对，不等式恒成立，求实数的取值范围．

    【答案】（1）；（2）．

    【解析】

    试题分析：（1）首先由零点的定义可得出关于的关系式，然后由二次函数的图像及其性质可得函数的最大值得出另一个关于的关系式，最后联立方程即可得出的值；（2）首先将已知转化为对恒成立，然后运用二次函数的图像及其性质可得出已知条件所满足的条件，进而得出所求的结果．

    试题解析：（1）的一个零点为-2，又当时最大值为0．即另一个零点在，则，即函数的两个零点分别为-2,4．

    或解：-2是零点，，

    当，即时，，（舍去）

    当，即时，，，此时

    （2）由（1）知, ，即对恒成立，则①或②

    解得①或 ②，综合得m的取值范围为．

    （注：亦可分离变量对恒成立）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为推行“微课、翻转课堂”教学法，某数学老师分别用传统教学和“微课、翻转课堂”两种不同的教学方式，在甲、乙两个平行班级进行教学实验，为了比较教学效果，期中考试后，分别从两个班级中各随机抽取20名学生的成绩进行统计，结果如下表：

    记成绩不低于70分者为“成绩优良”．

    （1）由以上统计数据填写下面列联表，并判断“成绩优良与教学方式是否有关”？

    附：

    临界值表：

    （2）现从上述40人中，学校按成绩是否优良采用分层抽样的方法抽取8人进行考核，在这8人中，记成绩不优良的乙班人数为，求的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学高三数学奥林匹克竞赛集训队的一次数学测试成绩的茎叶图（图1）和频率分布直方图（图2）都受到不同程度的破坏，可见部分如图所示，据此解答如下问题．

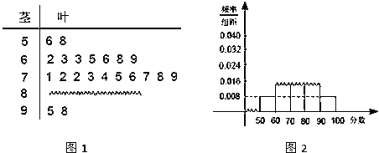
    （1）求该集训队总人数及分数在[80，90）之间的频数；

    （2）计算频率分布直方图中[80，90）的矩形的高；

    （3）若要从分数在[80，100]之间的试卷中任取两份分析学生的答题情况，在抽取的试卷中，求至少有一份分数在[90，100]之间的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】正方体的棱长为1,分别是棱，的中点，过直线的平面分别与棱、交于，设，，给出以下四个命题：

    ①四边形为平行四边形；

    ②若四边形面积,,则有最小值；

    ③若四棱锥的体积，，则为常函数；

    ④若多面体的体积，，则为单调函数．

    其中假命题为（ ）

    A．① ③ B．② C．③④ D．④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥，底面是、边长为的菱形，又底，且，点分别是棱的中点．

    （1）证明：平面；

    （2）证明：平面平面；

    （3）求点到平面的距离．[

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在锐角△ABC中，两向量p＝(2－2sin A，cos A＋sin A)，q＝(sin A－cos A,1＋sin A)，且p与q是共线向量.

    （1）求A的大小；

    （2）求函数y＝2sin2B＋cos（）取最大值时，角B的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中.

    （1）当时，求曲线在点处的切线的斜率；

    （2）当时，求函数的单调区间与极值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某投资商到一开发区投资72万元建起一座蔬菜加工厂，第一年共支出12万元，以后每年支出增加4万元，从第一年起每年的蔬菜销售收入均为50万元，设表示前年的纯利润总和（=前年的总收入前年的总支出投资额）.

    （1）该厂从第几年开始盈利？

    （2）若干年后，投资商为开发新项目，对该厂有两种处理方案：

    ① 当年平均利润达到最大时，以48万元出售该厂；

    ② 当纯利润总和达到最大时，以16万元出售该厂，

    问哪种方案更合算？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面是菱形，，侧面是边长为2的等边三角形，点是的中点，且平面平面．

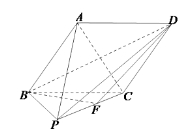
    （I）求异面直线与所成角的余弦值；

    （II）若点在线段上移动，是否存在点使平面与平面所成的角为？若存在，指出点的位置，否则说明理由．

    查看答案和解析>>

    同步练习册答案