
【题目】探究函数![]() ,x∈(0,+∞)取最小值时x的值,列表如下:
,x∈(0,+∞)取最小值时x的值,列表如下:
x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
请观察表中y值随x值变化的特点,完成以下的问题:
(1)函数![]() (x>0)在区间(0,2)上递减;函数
(x>0)在区间(0,2)上递减;函数![]() 在区间________上递增.当x=_________时,
在区间________上递增.当x=_________时,![]() _______.
_______.
(2)证明:函数![]() (x>0)在区间(O,2)上递减.
(x>0)在区间(O,2)上递减.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】(本小题共14分)
如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 是菱形,
是菱形, ![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]()
(Ⅱ)若![]() 求
求![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(Ⅲ)当平面![]() 与平面
与平面![]() 垂直时,求
垂直时,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于区间[a,b](a<b),若函数![]() 同时满足:①
同时满足:①![]() 在[a,b]上是单调函数,②函数
在[a,b]上是单调函数,②函数![]() 在[a,b]的值域是[a,b],则称区间[a,b]为函数
在[a,b]的值域是[a,b],则称区间[a,b]为函数![]() 的“保值”区间
的“保值”区间
(1)求函数![]() 的所有“保值”区间
的所有“保值”区间
(2)函数![]() 是否存在“保值”区间?若存在,求
是否存在“保值”区间?若存在,求![]() 的取值范围,若不存在,说明理由
的取值范围,若不存在,说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取![]() 个家庭,获得第
个家庭,获得第![]() 个家庭的月收入
个家庭的月收入![]() (单位:千元)与月储蓄
(单位:千元)与月储蓄![]() (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求家庭的月储蓄![]() 对月收入
对月收入![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判断变量![]() 与
与![]() 之间是正相关还是负相关;
之间是正相关还是负相关;
(3)若该居民区某家庭月收入为![]() 千元,预测该家庭的月储蓄.其中
千元,预测该家庭的月储蓄.其中![]() ,
,![]() 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为![]() ,附:线性回归方程
,附:线性回归方程![]() 中,
中, 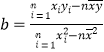 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知ABCD—A′B′C′D′是平行六面体.
(1)化简![]() ;
;
(2)设M是底面ABCD的中心,N是侧面BC C′ B′对角线B C′上的![]() 分点,设
分点,设![]() ,试求α,β,γ的值.
,试求α,β,γ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知,y对x呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一次函数![]() 是
是![]() 上的减函数,
上的减函数,![]() ,且 f [ f(x)]=16x-3.
,且 f [ f(x)]=16x-3.
(1)求![]() ;
;
(2)若![]() 在(-2,3)单调递增,求实数
在(-2,3)单调递增,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,
时,![]() 有最大值1,求实数
有最大值1,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体(如图):面ABCD为矩形,棱EF∥AB.若此几何体中,AB=4,EF=2,△ADE和△BCF都是边长为2的等边三角形,则此几何体的表面积为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣kx+k.
(Ⅰ)若f(x)≥0有唯一解,求实数k的值;
(Ⅱ)证明:当a≤1时,x(f(x)+kx﹣k)<ex﹣ax2﹣1.
(附:ln2≈0.69,ln3≈1.10, ![]() ,e2≈7.39)
,e2≈7.39)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com