解:(1)依题意,可设椭圆E的方程为

∵离心率为

,∴
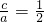
,即a=2c,
∴b
2=a
2-c
2=3c
2,
∵椭圆经过点

,∴

解得c
2=1
∴a
2=4,b
2=3
∴椭圆的方程为

.
(2)记A、B 两点坐标分别为A(x
1,x
2 ),B (x
2,y
2),
由
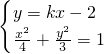
消去y,得 (4k
2+3)x
2-16kx+4=0,
∵直线与椭圆有两个交点,
∴△=(16k)
2-16(4k
2+3)>0,∴k
2>

,
由韦达定理 x
1 +x
2=
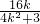
,x
1x
2=
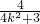
,
∵原点O在以MN为直径的圆外,∴∠MON为锐角
∵
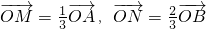
∴∠AOB为锐角
∴
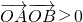
∵

═x
1x
2+y
1y
2=x
1x
2+(kx
1-2)(kx
2-2)=(k
2+1)x
1x
2-2k(x
1+x
2)+4
=(k
2+1)×
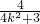
-2k×
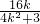
+4=
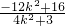
∴
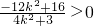
∴
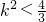
∵k
2>

,
∴
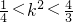
∴k的取值范围为
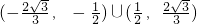
分析:(1)依题意设出椭圆的方程,根据离心率的值以及椭圆经过点

,待定系数法求出椭圆的方程;
(2)把直线的方程代入椭圆的方程,使用根与系数的关系,结合向量条件,原点O在以MN为直径的圆外,可得∠MON为锐角,从而∠AOB为锐角,利用向量的数量积,即可求得k的取值范围.
点评:本题考查椭圆的简单性质,用待定系数法求椭圆的方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查向量知识,综合性强.

 ,且经过点
,且经过点 .
.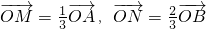 ,若原点O在以MN为直径的圆外,求k的取值范围.
,若原点O在以MN为直径的圆外,求k的取值范围.
 ,∴
,∴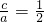 ,即a=2c,
,即a=2c, ,∴
,∴
 .
.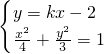 消去y,得 (4k2+3)x2-16kx+4=0,
消去y,得 (4k2+3)x2-16kx+4=0, ,
,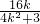 ,x1x2=
,x1x2=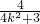 ,
,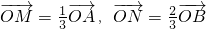
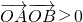
 ═x1x2+y1y2=x1x2+(kx1-2)(kx2-2)=(k2+1)x1x2-2k(x1+x2)+4
═x1x2+y1y2=x1x2+(kx1-2)(kx2-2)=(k2+1)x1x2-2k(x1+x2)+4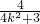 -2k×
-2k×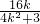 +4=
+4=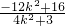
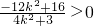
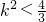
 ,
,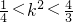
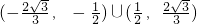
 ,待定系数法求出椭圆的方程;
,待定系数法求出椭圆的方程;

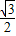 .
.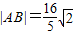 ,求直线l的方程.
,求直线l的方程.