练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在数列{an}中，a1＝2，an＋1＝4an－3n＋1，n∈N*.

    (1)求证：数列{an－n}是等比数列；

    (2)求数列{an}的前n项和Sn；

    (3)求证：不等式Sn＋1≤4Sn对任意n∈N*皆成立．

     

    （1）见解析（2）（3）见解析

    【解析】(1)证明：由题设an＋1＝4an－3n＋1，得an＋1－(n＋1)＝4(an－n)，n∈N*.又a1－1＝1，所以数列{an－n}是首项为1，公比为4的等比数列．

    (2)【解析】
    由    (1)可知an－n＝4n－1，于是数列{an}的通项公式为an＝4n－1＋n，所以数列{an}的前n项和Sn＝.

    (3)证明：对任意的n∈N*，Sn＋1－4Sn＝＝－ (3n2＋n－4)≤0，所以不等式Sn＋1≤4Sn对任意n∈N*皆成立．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第八章第1课时练习卷（解析版） 题型：解答题

    如图，四边形ABEF和ABCD都是直角梯形，∠BAD＝∠FAB＝90°，BC∥=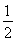AD，BE∥=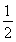FA，G、H分别为FA、FD的中点．

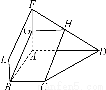
    (1)证明：四边形BCHG是平行四边形．

    (2)C、D、F、E四点是否共面？为什么？

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第4课时练习卷（解析版） 题型：解答题

    已知数列{an}的前n项和为Sn，对一切正整数n，点Pn(n，Sn)都在函数f(x)＝x2＋2x的图象上，且在点Pn(n，Sn)处的切线的斜率为kn.

    (1)求数列{an}的通项公式；

    (2)若bn＝2knan，求数列{bn}的前n项和Tn.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第3课时练习卷（解析版） 题型：解答题

    已知数列{an}的首项a1＝2a＋1(a是常数，且a≠－1)，

    an＝2an－1＋n2－4n＋2(n≥2)，数列{bn}的首项b1＝a，

    bn＝an＋n2(n≥2)．

    (1)证明：{bn}从第2项起是以2为公比的等比数列；

    (2)设Sn为数列{bn}的前n项和，且{Sn}是等比数列，求实数a的值；

    (3)当a>0时，求数列{an}的最小项．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第3课时练习卷（解析版） 题型：填空题

    已知数列{an}满足3an＋1＋an＝0，a2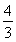＝－，则{an}的前10项和为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第3课时练习卷（解析版） 题型：填空题

    等比数列{an}中，a1>0，a2a4＋2a3a5＋a4a6＝36，则a3＋a5＝________．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第2课时练习卷（解析版） 题型：填空题

    设等差数列{an}的前n项和为Sn，Sm－1＝－2，Sm＝0，Sm＋1＝3，则m＝________．

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第五章第1课时练习卷（解析版） 题型：解答题

    若数列{an}满足an＋1＝an＋an＋2(n∈N*)，则称数列{an}为“凸数列”．

    (1)设数列{an}为“凸数列”，若a1＝1，a2＝－2，试写出该数列的前6项，并求出前6项之和；

    (2)在“凸数列”{an}中，求证：an＋3＝－an，n∈N*；

    (3)设a1＝a，a2＝b，若数列{an}为“凸数列”，求数列前2011项和S2011.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年高考数学总复习考点引领+技巧点拨第二章第8课时练习卷（解析版） 题型：解答题

    设a＞0，f(x)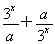＝是R上的偶函数．

    (1)求a的值；

    (2)判断并证明函数f(x)在[0，＋∞)上的单调性；

    (3)求函数的值域．

     

    查看答案和解析>>

    同步练习册答案