
����Ŀ������������ĸ����������
��![]() Ϊʵ������
Ϊʵ������![]() ��
��![]() ������Ƴ�:
������Ƴ�: ![]() Ϊ��������
��������![]() ��
��![]() .
.
�� ������![]() �ǵȲ����У�
�ǵȲ����У� ![]() ��������
��������![]() Ҳ�ǵȲ�����������Ƴ���������
Ҳ�ǵȲ�����������Ƴ���������![]() �Ǹ��Ϊ�����ĵȱ�������
�Ǹ��Ϊ�����ĵȱ������� ![]() ��������
��������![]() Ҳ�ǵȱ�����.
Ҳ�ǵȱ�����.
�� ��![]() ��
��![]() �� ����Ƴ�����
�� ����Ƴ�����![]() Ϊ������������
������������![]() .
.
�� ��Բ�İ뾶Ϊ![]() ,��Բ�����Ϊ
,��Բ�����Ϊ![]() ������Ƴ�������Բ�ij����᳤Ϊ
������Ƴ�������Բ�ij����᳤Ϊ![]() ,�̰��᳤Ϊ
,�̰��᳤Ϊ![]() ,����Բ�����Ϊ
,����Բ�����Ϊ![]() .�����ĸ������У�������ȷ���ǣ� ��
.�����ĸ������У�������ȷ���ǣ� ��
A. �� �� B. �� �� C. �� �� D. �� ��
���𰸡�D
�����������ڸ�����C�У���z1��z2��C��z12+z22=0�������z1=1��z2=i���ʴ���
������ȵȲ����е����������ȱ����е�����ʱ������һ���˼·�У��ɼӷ��������Ϊ�˷����ɼ����������Ϊ������������ƽ�����������Ϊ����ƽ�����ȣ������ǿ�������Ƴ���������{cn}�Ǹ��Ϊ�����ĵȱ����У�dn=![]() ��������{dn}Ҳ�ǵȱ����У���ȷ��
��������{dn}Ҳ�ǵȱ����У���ȷ��
������a��b��c��R��ab��c=a��bc��������Ƴ�����![]() Ϊ����������
Ϊ����������![]() .������ȷ����Ϊ
.������ȷ����Ϊ![]() ��
��![]() ���ߣ�
���ߣ� ![]() ��
��![]() ���ߣ���
���ߣ���![]() ��
��![]() ����ͬʱ���������������������ɲ�������
����ͬʱ���������������������ɲ�������
����Բ�İ뾶Ϊa����Բ�����Ϊ��a2������Ƴ�������Բ�ij����᳤Ϊa���̰��᳤Ϊb������Բ�����Ϊ��ab������Բ����Բ������������֤��֪��ȷ��
��ѡ��D��


 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() Ϊ���Ϊ
Ϊ���Ϊ![]() �ĵȲ����У�
�ĵȲ����У� ![]() Ϊǰ
Ϊǰ![]() ��ͣ�
��ͣ� ![]() ��
��![]() �ĵȲ�����Ϊ
�ĵȲ�����Ϊ![]() ����
����![]() ����
����![]() ����
����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ��
��
��1����![]() ��
��![]() ��
��
��2���Ƿ����������![]() �ɵȱ����У������ڣ�������е�
�ɵȱ����У������ڣ�������е�![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ������Ϊ19������Ϊ-2�ĵȲ�������
������Ϊ19������Ϊ-2�ĵȲ�������![]() Ϊ
Ϊ![]() ��ǰ
��ǰ![]() �����
�����
��1����ͨ��![]() ��
��![]() ��
��
��2����![]() ������Ϊ1������Ϊ3�ĵȱ�������������
������Ϊ1������Ϊ3�ĵȱ�������������![]() ��ͨ�ʽ����ǰ
��ͨ�ʽ����ǰ![]() ���
���![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ƽ��ֱ������ϵ![]() �У���ֱ֪��
�У���ֱ֪��![]() ����ͨ����Ϊ
����ͨ����Ϊ![]() ������
������![]() �IJ�������Ϊ
�IJ�������Ϊ ��
��![]() Ϊ����������ֱ��
Ϊ����������ֱ��![]() ������
������![]() ����
����![]() ��
�� ![]() ����.
����.
�������߶�![]() �ij���
�ij���
������֪��![]() ������
������![]() ���˶�����
���˶�����![]() ��������ʱ�����
��������ʱ�����![]() �����꼰
�����꼰![]() ��������.
��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��![]() ��
��![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ����.
����.
��������![]() ��
��![]() �ֱ���˫����
�ֱ���˫����![]() �����ᡢʵ���һ���˵㣬����ƽ����������
�����ᡢʵ���һ���˵㣬����ƽ����������![]() ��
��![]() ��ʹ��˫����
��ʹ��˫����![]() ������һ�㵽
������һ�㵽![]() ��
��![]() ����������ľ���ֵ�Ƕ�ֵ.
����������ľ���ֵ�Ƕ�ֵ.
��������ԭ��![]() ΪԲ�ĵ�Բ
ΪԲ�ĵ�Բ![]() ��ֱ��
��ֱ��![]() �����ҳ���
�����ҳ���![]() ����Բ
����Բ![]() �ķ����Լ������ҵ��е�.
�ķ����Լ������ҵ��е�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}Ϊ�Ȳ����У�����d��0������ ![]() ��
�� ![]() ������
������ ![]() ǡΪ�ȱ����У���k1=1��k2=5��k3=17����k1+k2+��+kn ��
ǡΪ�ȱ����У���k1=1��k2=5��k3=17����k1+k2+��+kn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��ǰn���Ϊ
��ǰn���Ϊ![]() ��
��![]() ���Ҷ�����������n����(
���Ҷ�����������n����(![]() ��
��![]() )��ֱ��
)��ֱ��![]() �ϣ�
�ϣ�
(1)������![]() ��ͨ�ʽ��
��ͨ�ʽ��
(2)�Ƿ����ʵ���ˣ�ʹ������{![]() }Ϊ�Ȳ����У������ڣ�����˵�ֵ���������ڣ���˵�����ɣ�
}Ϊ�Ȳ����У������ڣ�����˵�ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
�� ![]() ��
�� ![]() .
. ![]() ����
����![]() ƽ��
ƽ��![]() ��
�� ![]() ����
����![]() Ϊ
Ϊ![]() ������һ��.
������һ��.
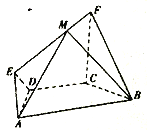
��1����֤�� ![]() ��
��
��2����![]() ���߶�
���߶�![]() ���˶����������˵㣩����ƽ��
���˶����������˵㣩����ƽ��![]() ��ƽ��
��ƽ��![]() ���ɵ�������Ϊ60�㣬��ȷ����
���ɵ�������Ϊ60�㣬��ȷ����![]() ��λ�ã�
��λ�ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ǡ�ABC���������3 ![]() ����AB=3��AC=4��
����AB=3��AC=4��
��1����sin�� ![]() +A����ֵ��
+A����ֵ��
��2����cos��A��B����ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com