
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]() .
.
(1)求sinBsinC;
(2)若3cosB(sin2A+sin2B﹣sin2C)=sinAsinB,a=6,求b+c的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用面积公式,结合正弦定理将边化角,即可整理化简求得结果;
(2)利用余弦定理,结合已知条件,求得![]() ,再结合(1)中所求,求得角
,再结合(1)中所求,求得角![]() ;然后用余弦定理和
;然后用余弦定理和![]() ,求得
,求得![]() 的结果.
的结果.
(1)由三角形的面积公式可得
S△ABC![]() acsinB
acsinB![]() ,
,
∴3csinBsinB=2b,
由正弦定理可得:3sinCsinBsinB=2sinB,
∵sinB≠0,
∴sinBsinC![]() ;
;
(2)∵3cosB(sin2A+sin2B﹣sin2C)=sinAsinB,
∴由正弦定理可得:3cosB(a2+b2﹣c2)=ab,
可得:3cosB2abcosC=ab,
故cosBcosC![]() ,
,
∴cos(B+C)=cosBcosC﹣sinBsinC![]() ,
,
∴B+C![]() ,可得A
,可得A![]() ,
,
∵a=6,
∴36=b2+c2﹣bc=(b+c)2﹣3bc,即:(b+c)2=36+3bc,
又∵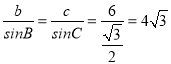 ,可得:b=4
,可得:b=4![]() sinB,c=4
sinB,c=4![]() sinC,
sinC,
∴bc=48sinBsinC=48![]() 32,
32,
∴![]() =36+3bc=36+96=132,
=36+3bc=36+96=132,
解得:b+c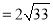 .
.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源: 题型:
【题目】己知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别是椭圈
分别是椭圈![]() 的左、右焦点,椭圆
的左、右焦点,椭圆![]() 的焦点
的焦点![]() 到双曲线
到双曲线![]() 渐近线的距离为
渐近线的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,以线段
两点,以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,且原点
,且原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角极坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() 其中
其中![]() 为参数,其中
为参数,其中![]() 为
为![]() 的倾斜角,且其中
的倾斜角,且其中![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立平面直角坐标系,曲线C1的极坐标方程
轴的正半轴为极轴建立平面直角坐标系,曲线C1的极坐标方程![]() ,曲线C2的极坐标方程
,曲线C2的极坐标方程![]() .
.
(1)求C1、C2的直角坐标方程;
(2)已知点P(-2,0),![]() 与C1交于点
与C1交于点![]() ,与C2交于A,B两点,且
,与C2交于A,B两点,且![]() ,求
,求![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知曲线![]() :
:![]() 和曲线
和曲线![]() :
:![]() ,以极点
,以极点![]() 为坐标原点,极轴为
为坐标原点,极轴为![]() 轴非负半轴建立平面直角坐标系.
轴非负半轴建立平面直角坐标系.
(1)求曲线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 是曲线
是曲线![]() 上一动点,过点
上一动点,过点![]() 作线段
作线段![]() 的垂线交曲线
的垂线交曲线![]() 于点
于点![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为降低养殖户养鸭风险,某保险公司推出了鸭意外死亡保险,该保单合同规定每只幼鸭投保2元,若生长期内鸭意外死亡,则公司每只鸭赔付12元.假设鸭在生长期内的意外死亡率为0.15,且每只鸭是否死亡相互独立.若某养殖户养鸭3000只,都投保该险种.
(1)求该保单保险公司赔付金额等于保费时,鸭死亡的只数;
(2)求该保单保险公司平均获利多少元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图几何体是圆锥的一部分,它是Rt△ABC(及其内部)以一条直角边AB所在直线为旋转轴旋转150°得到的,AB=BC=2,P是弧![]() 上一点,且EB⊥AP.
上一点,且EB⊥AP.
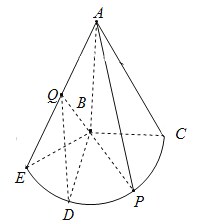
(1)求∠CBP的大小;
(2)若Q为AE的中点,D为弧![]() 的中点,求二面角Q﹣BD﹣P的余弦值;
的中点,求二面角Q﹣BD﹣P的余弦值;
(3)直线AC上是否存在一点M,使得B、D、M、Q四点共面?若存在,请说明点M的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校开展的高二“学工学农”某天的活动安排中,有采茶,摘樱桃,摘草莓,锄草,栽树,喂奶牛共六项活动可供选择,每个班上午,下午各安排一项(不重复),且同一时间内每项活动都只允许一个班参加,则该天甲,乙两个班的活动安排方案的种数为:________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】基于移动网络技术的共享单车被称为“新四大发明”之一,短时间内就风靡全国,给人们带来新的出行体验,某共享单车运营公司的市场研究人员为了了解公司的经营状况,对公司最近6个月的市场占有率![]() 进行了统计,结果如下表:
进行了统计,结果如下表:
月份 | 2018.11 | 2018.12 | 2019.01 | 2019.02 | 2019.03 | 2019.04 |
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
| 11 | 13 | 16 | 15 | 20 | 21 |
(1)请用相关系数说明能否用线性回归模型拟合![]() 与月份代码
与月份代码![]() 之间的关系.如果能,请计算出
之间的关系.如果能,请计算出![]() 关于
关于![]() 的线性回归方程,如果不能,请说明理由;
的线性回归方程,如果不能,请说明理由;
(2)根据调研数据,公司决定再采购一批单车扩大市场,从成本1000元/辆的![]() 型车和800元/辆的
型车和800元/辆的![]() 型车中选购一种,两款单车使用寿命频数如下表:
型车中选购一种,两款单车使用寿命频数如下表:
| 1年 | 2年 | 3年 | 4年 | 总计 |
| 10 | 30 | 40 | 20 | 100 |
| 15 | 40 | 35 | 10 | 100 |
经测算,平均每辆单车每年能为公司带来500元的收入,不考虑除采购成本以外的其它成本,假设每辆单车的使用寿命都是整数年,用频率估计每辆车使用寿命的概率,以平均每辆单车所产生的利润的估计值为决策依据,如果你是公司负责人,会选择哪款车型?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数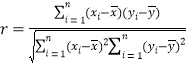 ,
, ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com