
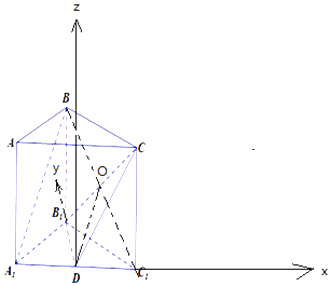
【题目】如图所示,三棱柱ABC﹣A1B1C1的底面是边长为2正三角形,D是A1C1的中点,且AA1⊥平面ABC,AA1=3.
(Ⅰ)求证:A1B∥平面B1DC;
(Ⅱ)求二面角D﹣B1C﹣C1的余弦值.
【答案】证明:(Ⅰ)连结BC1,B1C,交于点O,连结OD,
∵三棱柱ABC﹣A1B1C1的底面是边长为2正三角形,D是A1C1的中点,
∴OD∥A1B,
∵A1B平面B1DC,OD平面B1DC,
∴A1B∥平面B1DC.
(Ⅱ)∵三棱柱ABC﹣A1B1C1的底面是边长为2正三角形,D是A1C1的中点,且AA1⊥平面ABC,AA1=3.
∴以D为原点,DC1为x轴,DB1为y轴,过D作平面A1B1C1的垂线为z轴,建立空间直角坐标系,
则D(0,0,0),B1(0, ![]() ,0),C(1,0,3),C1(1,0,0),
,0),C(1,0,3),C1(1,0,0),
![]() =(﹣1,
=(﹣1, ![]() ,﹣3),
,﹣3), ![]() =(﹣1,0,﹣3),
=(﹣1,0,﹣3), ![]() =(0,0,﹣3),
=(0,0,﹣3),
设平面B1DC的法向量 ![]() =(x,y,z),
=(x,y,z),
则 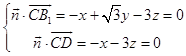 ,取z=1,得
,取z=1,得 ![]() =(﹣3,0,1),
=(﹣3,0,1),
设平面B1CC1的法向量 ![]() =(a,b,c),
=(a,b,c),
则 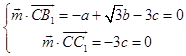 ,取b=1,得
,取b=1,得 ![]() =(
=( ![]() ),
),
设二面角D﹣B1C﹣C1的平面角为θ,
则cosθ= ![]() =
= ![]() =
= ![]() .
.
∴二面角D﹣B1C﹣C1的余弦值为 ![]() .
.
【解析】(Ⅰ)连结BC1,B1C,交于点O,连结OD,则OD∥A1B,由此能证明A1B∥平面B1DC.(Ⅱ)以D为原点,DC1为x轴,DB1为y轴,过D作平面A1B1C1的垂线为z轴,建立空间直角坐标系,利用向量法能求出二面角D﹣B1C﹣C1的余弦值.
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 且S5=a5+a6=25.
(1)求{an}的通项公式;
(2)若不等式2Sn+8n+27>(﹣1)nk(an+4)对所有的正整数n都成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB=BE=BC=2AD=2,且AB⊥BE,∠DAB=60°,AD∥BC,BE⊥AD,
(Ⅰ)求证:面ADE⊥面 BDE;
(Ⅱ)求直线AD与平面DCE所成角的正弦值..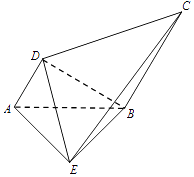
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=|x+a|,g(x)=|x+3|﹣x,记关于x的不等式f(x)<g(x)的解集为M.
(1)若a﹣3∈M,求实数a的取值范围;
(2)若[﹣1,1]M,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期为4π,且对x∈R,有f(x)≤f(
)的最小正周期为4π,且对x∈R,有f(x)≤f( ![]() )成立,则关于函数f(x)的下列说法中正确的是( )
)成立,则关于函数f(x)的下列说法中正确的是( )
①φ= ![]()
②函数f(x)在区间[﹣π,π]上递减;
③把g(x)=sin ![]() 的图象向左平移
的图象向左平移 ![]() 得到f(x)的图象;
得到f(x)的图象;
④函数f(x+ ![]() )是偶函数.
)是偶函数.
A.①③
B.①②
C.②③④
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x1 , x2 , x3 , x4},xi∈{﹣1,0,1},i={1,2,3,4},那么集合A中满足条件“x12+x22+x32+x42≤3”的元素个数为( )
A.60
B.65
C.80
D.81
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究学生的数学核素养与抽象(能力指标x)、推理(能力指标y)、建模(能力指标z)的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标w=x+y+z的值评定学生的数学核心素养;若w≥7,则数学核心素养为一级;若5≤w≤6,则数学核心素养为二级;若3≤w≤4,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下结果:
学生编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
(x,y,z) | (2,2,3) | (3,2,3) | (3,3,3) | (1,2,2) | (2,3,2) | (2,3,3) | (2,2,2) | (2,3,3) | (2,1,1) | (2,2,2) |
(1)在这10名学生中任取两人,求这两人的建模能力指标相同的概率;
(2)从数学核心素养等级是一级的学生中任取一人,其综合指标为a,从数学核心素养等级不是一级的学生中任取一人,其综合指标为b,记随机变量X=a﹣b,求随机变量X的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|x﹣a|,a∈R
(Ⅰ)当a=5,解不等式f(x)≤3;
(Ⅱ)当a=1时,若x∈R,使得不等式f(x﹣1)+f(2x)≤1﹣2m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,已知|AB|=|AC|=1,∠A=120°,E,F分别是AB,AC上的点,且 ![]() ,(其中λ,μ∈(0,1)),且λ+4μ=1,若线段EF,BC的中点分别为M,N,则
,(其中λ,μ∈(0,1)),且λ+4μ=1,若线段EF,BC的中点分别为M,N,则 ![]() 的最小值为 .
的最小值为 . 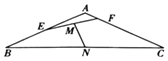
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com