
【题目】已知椭圆C: ![]() 的上下焦点分别为F1 , F2 , 离心率为
的上下焦点分别为F1 , F2 , 离心率为 ![]() ,P为C上动点,且满足
,P为C上动点,且满足 ![]() |,△QF1F2面积的最大值为4. (Ⅰ)求Q点轨迹E的方程和椭圆C的方程;
|,△QF1F2面积的最大值为4. (Ⅰ)求Q点轨迹E的方程和椭圆C的方程;
(Ⅱ)直线y=kx+m(m>0)与椭圆C相切且与曲线E交于M,N两点,求 ![]() 的取值范围.
的取值范围.
【答案】解:(Ⅰ)由椭圆定义得:|F2Q|=|F2P|+|PQ|=|F2P|+|PF1|=2a, 所以点Q的轨迹是以F2为圆心,2a为半径的圆.
当QF2⊥F1F2时△QF1F2面积最大,所以 ![]() 得:ac=2
得:ac=2
又 ![]() 可得a=2,c=1.
可得a=2,c=1.
所以Q点轨迹E的方程x2+(y+1)2=16,椭圆C的方程 ![]()
(Ⅱ)由 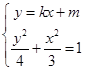 得(3k2+4)x2+6kmx+3m2﹣12=0△=36k2m2﹣4(3k2+4)(3m2﹣12)=0
得(3k2+4)x2+6kmx+3m2﹣12=0△=36k2m2﹣4(3k2+4)(3m2﹣12)=0
化简得:3k2﹣m2+4=0
所以, ![]()
由 ![]() 及m>0得,m≥2
及m>0得,m≥2
设圆心F2(0,﹣1)到直线MN的距离为d,则 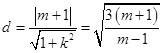
所以,弦长 ![]()
设点F1(0,1)到直线MN的距离为h,则 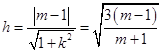
所以, ![]()
由m≥2,得: ![]()
所以, ![]() 的取值范围为
的取值范围为 ![]() .
.
【解析】(Ⅰ)由椭圆定义得:|F2Q|=|F2P|+|PQ|=|F2P|+|PF1|=2a,点Q的轨迹是以F2为圆心,2a为半径的圆,当QF2⊥F1F2时△QF1F2面积最大,推出ac=2,结合离心率,然后求解椭圆方程即可.(Ⅱ)联立 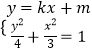 通过△=0,推出
通过△=0,推出 ![]() 求出m≥2,设圆心F2(0,﹣1)到直线MN的距离为d,求出弦长,设点F1(0,1)到直线MN的距离为h,求出三角形的面积的表达式,然后求解范围即可.
求出m≥2,设圆心F2(0,﹣1)到直线MN的距离为d,求出弦长,设点F1(0,1)到直线MN的距离为h,求出三角形的面积的表达式,然后求解范围即可.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 满足
满足![]() .
.
(Ⅰ)当![]() 时,解不等式
时,解不等式![]() ;
;
(Ⅱ)若关于x的方程![]() 的解集中有且只有一个元素,求a的值;
的解集中有且只有一个元素,求a的值;
(Ⅲ)设![]() ,若对
,若对![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求a的取值范围.
上的最大值与最小值的差不超过1,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面几何中,通常将完全覆盖某平面图形且直径最小的圆,称为该平面图形的最小覆盖圆.最小覆盖圆满足以下性质:①线段![]() 的最小覆盖圆就是以
的最小覆盖圆就是以![]() 为直径的圆;②锐角
为直径的圆;②锐角![]() 的最小覆盖圆就是其外接圆.已知曲线
的最小覆盖圆就是其外接圆.已知曲线![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为曲线
为曲线![]() 上不同的四点.
上不同的四点.
(Ⅰ)求实数![]() 的值及
的值及![]() 的最小覆盖圆的方程;
的最小覆盖圆的方程;
(Ⅱ)求四边形![]() 的最小覆盖圆的方程;
的最小覆盖圆的方程;
(Ⅲ)求曲线![]() 的最小覆盖圆的方程.
的最小覆盖圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举办“中国诗词大赛”活动,某班派出甲乙两名选手同时参加比赛.大赛设有15个诗词填空题,其中“唐诗”、“宋词”和“毛泽东诗词”各5个.每位选手从三类诗词中各任选1个进行作答,3个全答对选手得3分,答对2个选手得2分,答对1个选手得1分,一个都没答对选手得0分.已知“唐诗”、“宋词”和“毛泽东诗词”中甲能答对的题目个数依次为5,4,3,乙能答对的题目个数依此为4,5,4,假设每人各题答对与否互不影响,甲乙两人答对与否也互不影响. 求:
(Ⅰ)甲乙两人同时得到3分的概率;
(Ⅱ)甲乙两人得分之和ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() ,解不等式
,解不等式![]() ;
;
(Ⅱ)设![]() 是函数
是函数![]() 的四个不同的零点,问是否存在实数
的四个不同的零点,问是否存在实数![]() ,使得其中三个零点成等差数列?若存在,求出所有
,使得其中三个零点成等差数列?若存在,求出所有![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com