
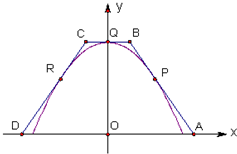
 如图,等腰梯形ABCD的三边AB,BC,CD分别与函数
如图,等腰梯形ABCD的三边AB,BC,CD分别与函数 ,x∈[-2,2]的图象切于点P,Q,R.求梯形ABCD面积的最小值.
,x∈[-2,2]的图象切于点P,Q,R.求梯形ABCD面积的最小值. .
. ,∴y'=-x∴y'|x=t=-t
,∴y'=-x∴y'|x=t=-t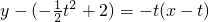 ,
,
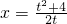 ,∴
,∴ .
. ∴
∴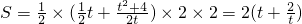
 …
… ,即
,即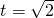 时,取“=”且
时,取“=”且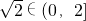 ,∴
,∴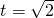 时,S有最小值为
时,S有最小值为 .∴梯形ABCD的面积的最小值为
.∴梯形ABCD的面积的最小值为
 ,我们易求出直线AB的方程,进而求出A,B的坐标,进而得到梯形的上底、下底及高,代入梯形面积公式,利用基本不等式求出最值即可得到答案.
,我们易求出直线AB的方程,进而求出A,B的坐标,进而得到梯形的上底、下底及高,代入梯形面积公式,利用基本不等式求出最值即可得到答案.

科目:高中数学 来源: 题型:
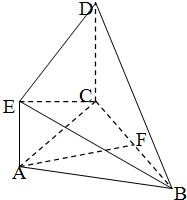 (2013•惠州一模)如图,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2
(2013•惠州一模)如图,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2查看答案和解析>>
科目:高中数学 来源:云南省建水一中2012届高三10月月考数学文科试题 题型:044
如图,等腰梯形ABCD中,2BC=AD=3,过B作AD的垂线,垂足为O,且OB=BC,沿着垂线OB将△AOB折起,使平面AOB⊥平面OBCD

(1)证明:平面AOC⊥平面ABC
(2)若E是AD中点,求四面体A=OCE的体积
查看答案和解析>>
科目:高中数学 来源:2011年湖南省高二数学选修4-1《几何证明选讲》单元练习题 题型:解答题
已知:如右图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证:(1)△ABC≌△DCB (2)DE·DC=AE·BD.
查看答案和解析>>
科目:高中数学 来源:2013届度辽宁省高二12月月考数学试题 题型:解答题
已知:如右图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.求证:(1)△ABC≌△DCB (2)DE·DC=AE·BD.

查看答案和解析>>
科目:高中数学 来源:2010年新疆农七师高级中学高二第二学期第二阶段考试数学(文)试题 题型:解答题
(本小题满分12分)已知:如右图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.

求证:(1)△ABC≌△DCB
(2)DE·DC=AE·BD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com