
【题目】如图,已知F是抛物线C:![]() 的焦点,过E(﹣l,0)的直线
的焦点,过E(﹣l,0)的直线![]() 与抛物线分別交于A,B两点(点A,B在x轴的上方).
与抛物线分別交于A,B两点(点A,B在x轴的上方).
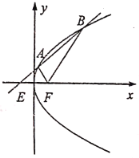
(1)设直线AF,BF的斜率分別为![]() ,
,![]() ,证明:
,证明:![]() ;
;
(2)若![]() ABF的面积为4,求直线
ABF的面积为4,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】设函数![]() (a,b
(a,b![]() R)的导函数为
R)的导函数为![]() ,已知
,已知![]() ,
,![]() 是
是![]() 的两个不同的零点.
的两个不同的零点.
(1)证明:![]() ;
;
(2)当b=0时,若对任意x>0,不等式![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(3)求关于x的方程![]() 的实根的个数.
的实根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台为了了解某社区居民对某娱乐节目的收视情况,随机抽取了![]() 名观众进行调查,下面是根据调查结果绘制的观众日均收看该娱乐节目时间的频率分布直方图:
名观众进行调查,下面是根据调查结果绘制的观众日均收看该娱乐节目时间的频率分布直方图:
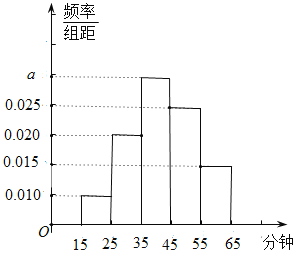
(1)求实数![]() 的值;
的值;
(2)根据统计结果,试估计观众观看该娱乐节目时间的中位数(结果保留一位小数);
(3)从观看时间在![]() ,
,![]() 的人中用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人的观看时间都在
的人中用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人的观看时间都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,![]() ,四边形BDEF是矩形,平面
,四边形BDEF是矩形,平面![]() 平面ABCD,
平面ABCD,![]() ,H是CF的中点.
,H是CF的中点.

(1)求证:![]() 平面BDEF;
平面BDEF;
(2)求直线DH与平面CEF所成角的正弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教材曾有介绍:圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() .我们将其结论推广:椭圆
.我们将其结论推广:椭圆![]() (
(![]() )上的点
)上的点![]() 处的切线方程为
处的切线方程为![]() ,在解本题时可以直接应用.已知,直线
,在解本题时可以直接应用.已知,直线![]() 与椭圆
与椭圆![]() :
:![]() (
(![]() )有且只有一个公共点.
)有且只有一个公共点.
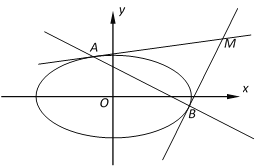
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过椭圆
为坐标原点,过椭圆![]() 上的两点
上的两点![]() 、
、![]() 分别作该椭圆的两条切线
分别作该椭圆的两条切线![]() 、
、![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() .当
.当![]() 变化时,求
变化时,求![]() 面积的最大值;
面积的最大值;
(3)若![]() 是椭圆
是椭圆![]()
![]() 上不同的两点,
上不同的两点,![]()
![]() 轴,圆
轴,圆![]() 过
过![]() 且椭圆
且椭圆![]() 上任意一点都不在圆
上任意一点都不在圆![]() 内,则称圆
内,则称圆![]() 为该椭圆的一个内切圆.试问:椭圆
为该椭圆的一个内切圆.试问:椭圆![]() 是否存在过左焦点
是否存在过左焦点![]() 的内切圆?若存在,求出圆心
的内切圆?若存在,求出圆心![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|1-a≤x≤1+a}(a>0),B={x|x2-5x+4≤0}.
(1)若“x∈A”是“x∈B”的必要不充分条件,求实数a的取值范围;
(2)对任意x∈B,不等式x2-mx+4≥0都成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com