
【题目】已知函数![]() 是偶函数.
是偶函数.
(1)求![]() 的值;
的值;
(2)若函数![]() 的图像与直线
的图像与直线![]() 没有交点,求
没有交点,求![]() 的取值范围;
的取值范围;
(3)若函数![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() 最小值为0,若存在,求出
最小值为0,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】袋子里有编号为![]() 的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
甲说:“我无法确定.”
乙说:“我也无法确定.”
甲听完乙的回答以后,甲又说:“我可以确定了.”
根据以上信息, 你可以推断出抽取的两球中
A. 一定有3号球 B. 一定没有3号球 C. 可能有5号球 D. 可能有6号球
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是R上的可导函数,对于任意的正实数t,都有函数g(x)=f(x+t)﹣f(x)在其定义域内为减函数,则函数y=f(x)的图象可能为如图中( )
A.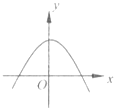
B.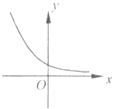
C.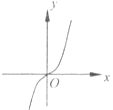
D.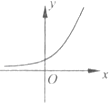
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是各项均不为0的等差数列.Sn为其前n项和,且满足an2=S2n﹣1(n∈N*),bn=an2+λan , 若{bn}为递增数列,则实数λ的范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:ax﹣y+1=0与x轴,y轴分别交于点A,B.
(1)若a>0,点M(1,﹣1),点N(1,4),且以MN为直径的圆过点A,求以AN为直径的圆的方程;
(2)以线段AB为边在第一象限作等边三角形ABC,若a=﹣ ![]() ,且点P(m,
,且点P(m, ![]() )(m>0)满足△ABC与△ABP的面积相等,求m的值.
)(m>0)满足△ABC与△ABP的面积相等,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(4,﹣3),B(2,﹣1)和直线l:4x+3y﹣2=0.
(1)求在直角坐标平面内满足|PA|=|PB|的点P的方程;
(2)求在直角坐标平面内一点P满足|PA|=|PB|且点P到直线l的距离为2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com