
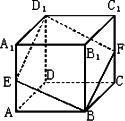
如图,已知E,F分别是正方体ABCD-A1B1C1D1的棱AA1和棱CC1上的点,且AE=C1F,求证:四边形EBFD1是平行四边形.
|
证明:如图,在棱DD1上取一点G,使D1G=A1E. 又因为A1E∥D1G, 所以四边形A1EGD1为平行四边形, 所以EG∥A1D1,且EG=A1D1. 又因为A1D1∥BC,且A1D1=BC, 所以EG∥BC,且EG=BC, 所以四边形EBCG为平行四边形, 所以EB∥GC,且EB=GC. 又因为D1G=A1E,AE=C1F,AA1=CC1, 所以D1G=FC. 又因为D1G∥FC, 所以四边形D1GCF为平行四边形, 所以GC∥D1F,且GC=D1F. 所以EB∥D1F,且EB=D1F. 所以四边形EBFD1为平行四边形.
点评:对于空间几何中的两直线a,b,如果很难直接判断它们是否平行,可利用a∥c与b∥c证得(即运用公理4证明). |


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:044
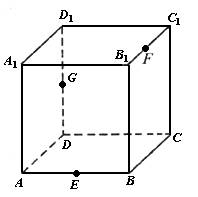
如图,已知E,F与G分别为正方体ABCD-A1B1C1D1棱AB、B1C1与DD1上的一点,试过E、F、G三点作正方体ABCD-A1B1C1D1的截面.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044

查看答案和解析>>
科目:高中数学 来源:导学大课堂选修数学2-1苏教版 苏教版 题型:047
如图,已知E、F、G、H、K、L分别为正方体AC1的棱,AA1、BB、BC、CC1、C1D1、A1D1的中点,求证:EF、GH、KL三线共面.

查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求证:E、F、G、H四点共面;
(2)求证:BD//平面EFGH;
(3)设M是EG和FH的交点,求证:对于空间任意一点O有
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com