
【题目】为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将所得的数据整理后,画频率分布直方图.已知图中横轴从左向右的分组为[50,75)、[75,100)、[100,125)、[125,150],纵轴前3个对应值分别为0.004、0.01、0.02,因失误第4个对应值丢失. 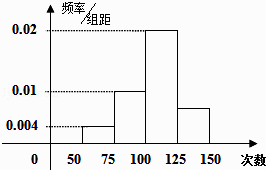
(Ⅰ) 已知第1小组频数为10,求参加这次测试的人数?
(Ⅱ) 求第4小组在y轴上的对应值;
(Ⅲ) 若次数在75次以上 ( 含75次 ) 为达标,试估计该年级跳绳测试达标率是多少?
(Ⅳ) 试估计这些数据的中位数.
【答案】解:(Ⅰ)参加这次测试的人数为 ![]() ; (Ⅱ)1﹣(0.004+0.01+0.02)×25=0.15,对应值为
; (Ⅱ)1﹣(0.004+0.01+0.02)×25=0.15,对应值为 ![]() ;
;
(Ⅲ)1﹣0.004×25=0.9,所以达标率为90%;
(Ⅳ)第一组的频率为0.1,第二组的频率为0.25,第三组的频率为0.5,所以中位数在第三组,0.5﹣0.1﹣0.25=0.15,所以 ![]() ,所以中位数为107.5
,所以中位数为107.5
【解析】(Ⅰ)由学生总数=第一组的频数÷频率计算;(Ⅱ)由频率之和等于1可求得第四组的频率;(Ⅲ)利用1减去第一组的频率即可求解;(Ⅳ)由中位数的概念分析.
【考点精析】认真审题,首先需要了解频率分布直方图(频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息).


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(1+x)﹣x,g(x)=xlnx.
(1)求函数f(x)的最大值;
(2)设0<a<b,证明0<g(a)+g(b)﹣2g( ![]() )<(b﹣a)ln2.
)<(b﹣a)ln2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1= ![]() ,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 .
,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 . 
(1)证明:BC⊥AB1;
(2)若OC=OA,求直线C1D与平面ABC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=xex﹣ax2﹣x,a∈R.
(1)当a= ![]() 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(2)若对x≥1时,恒有f(x)≥xex+ax2成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,从椭圆 ![]() 上一点P向x轴作垂线,垂足恰为左焦点F1 , 又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且
上一点P向x轴作垂线,垂足恰为左焦点F1 , 又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且 ![]() . (Ⅰ) 求椭圆的方程;
. (Ⅰ) 求椭圆的方程;
(Ⅱ) 若M是椭圆上的动点,点N(4,2),求线段MN中点Q的轨迹方程.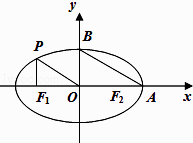
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+x2(a为实常数).
(1)当a=﹣4时,求函数f(x)在[1,e]上的最大值及相应的x值;
(2)当x∈[1,e]时,讨论方程f(x)=0根的个数.
(3)若a>0,且对任意的x1 , x2∈[1,e],都有 ![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥V﹣ABCD中,底面ABCD是边长2为的正方形,其他四个侧面都是侧棱长为 ![]() 的等腰三角形.
的等腰三角形. 
(1)求正四棱锥V﹣ABCD的体积.
(2)求二面角V﹣BC﹣A的平面角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com