
【题目】定义在(﹣∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{an},{f(an)}仍是等比数列,则称f(x)为“保等比数列函数”.现有定义在(﹣∞,0)∪(0,+∞)上的如下函数:①f(x)=x2;②f(x)=2x;③f(x)= ![]() ;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为( )
;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为( )
A.①②
B.③④
C.①③
D.②④
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】某校倡导为特困学生募捐,要求在自动购水机处每购买一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出矿泉水箱数和收入情况,列表如下:
售出水量 | 7 | 6 | 6 | 5 | 6 |
收入 | 165 | 142 | 148 | 125 | 150 |
学校计划将捐款以奖学金的形式奖励给品学兼优的特困生,规定:特困生综合考核前20名,获一等奖学金500元;综合考核21-50名,获二等奖学金300元;综合考核50名以后的不获得奖学金.
(1)若![]() 与
与![]() 成线性相关,则某天售出9箱水时,预计收入为多少元?
成线性相关,则某天售出9箱水时,预计收入为多少元?
(2)甲乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() ,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和
,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和![]() 的分布列及数学期望;
的分布列及数学期望;
附:回归方程![]() ,其中
,其中 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设ξ为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,ξ=0;当两条棱平行时,ξ的值为两条棱之间的距离;当两条棱异面时,ξ=1.
(1)求概率P(ξ=0);
(2)求ξ的分布列,并求其数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
一次性购物量 | 1至4件 | 5 至8件 | 9至12件 | 13至16件 | 17件及以上 |
顾客数(人) | x | 30 | 25 | y | 10 |
结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
已知这100位顾客中的一次购物量超过8件的顾客占55%.
(1)确定x,y的值,并求顾客一次购物的结算时间X的分布列与数学期望;
(2)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2.5分钟的概率.(注:将频率视为概率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业接到生产3000台某产品的A,B,C三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件).已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为K(K为正整数).
(1)设生产A部件的人数为x,分别写出完成A,B,C三种部件生产需要的时间;
(2)假设这三种部件的生产同时开工,试确定正整数K的值,使完成订单任务的时间最短,并给出时间最短时具体的人数分组方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 有以下性质:
有以下性质:
①过圆![]() 上一点
上一点![]() 的圆的切线方程是
的圆的切线方程是![]() .
.
②若不在坐标轴上的点![]() 为圆
为圆![]() 外一点,过
外一点,过![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,则
,则![]() 垂直
垂直![]() ,即
,即![]() .
.
(1)类比上述有关结论,猜想过椭圆![]() 上一点
上一点![]() 的切线方程 (不要求证明);
的切线方程 (不要求证明);
(2)若过椭圆![]() 外一点
外一点![]() (
(![]() 不在坐标轴上)作两直线,与椭圆相切于
不在坐标轴上)作两直线,与椭圆相切于![]() 两点,求证:
两点,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个顶点为
的一个顶点为![]() ,且它的离心率与双曲线
,且它的离心率与双曲线![]() 的离心率互为倒数.
的离心率互为倒数.
(1)求椭圆的方程;
(2)过点A且斜率为k的直线l与椭圆相交于A,B两点,点M在椭圆上,且满![]() 求k的值.
求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】首届中国国际进口博览会在2018年11月5日—10日在上海国家会展中心举办。会议期间,某公司欲采购东南亚某水果种植基地的水果,公司刘总经理与该种植基地的负责人陈老板商定一次性采购一种水果的采购价![]() (元/吨)与采购量
(元/吨)与采购量![]() (吨)之间的函数关系的图象如图中的折线
(吨)之间的函数关系的图象如图中的折线![]() 所示(不包含端点
所示(不包含端点![]() ,但包含端点
,但包含端点![]() ).
).
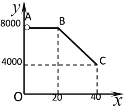
(Ⅰ)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(Ⅱ)已知该水果种植基地种植该水果的成本是2800元/吨,那么刘总经理的采购量为多少时,该水果基地在这次买卖中所获得利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com