
【题目】如图,下列4个正方体中,点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为正方体的顶点或所在棱的中点,则在这4个正方体中,满足直线
分别为正方体的顶点或所在棱的中点,则在这4个正方体中,满足直线![]() 平面
平面![]() 的个数为( )
的个数为( )
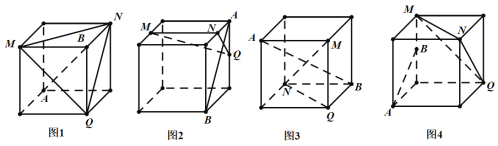
A.1B.2C.3D.4
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量速率,(单位:![]() )与管道半径r(单位:cm)的四次方成正比.
)与管道半径r(单位:cm)的四次方成正比.
(1)写出气体流量速率,关于管道半径r的函数解析式;
(2)若气体在半径为3cm的管道中,流量速率为![]() ,求该气体通过半径为r的管道时,其流量速率v的表达式;
,求该气体通过半径为r的管道时,其流量速率v的表达式;
(3)已知(2)中的气体通过的管道半径为5cm,计算该气体的流量速率(精确到![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线![]() 相切,过点
相切,过点![]() 且不垂直于
且不垂直于![]() 轴直线
轴直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点。
两点。
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 关于
关于![]() 轴的对称点是点
轴的对称点是点![]() ,证明:直线
,证明:直线![]() 与
与![]() 轴相交于定点。
轴相交于定点。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,且
,且![]() ,
,![]() 为
为![]() 中点.
中点.
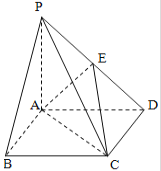
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得点
,使得点![]() 到平
到平
面![]() 的距离为
的距离为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;
的位置;
若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据某镇家庭抽样调查的统计,2003年每户家庭平均消费支出总额为1万元,其中食品消费额为0.6万元.预测2003年后,每户家庭平均消费支出总额每年增加3000元,如果到2005年该镇居民生活状况能达到小康水平(即恩格尔系数n满足![]() ),则这个镇每户食品消费额平均每年的增长率至多是多少(精确到0.1%)?
),则这个镇每户食品消费额平均每年的增长率至多是多少(精确到0.1%)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com