
分析 (1)根据 $\overrightarrow{AB}•\overrightarrow{BC}$=0,以及$\overrightarrow{a}•\overrightarrow{b}$=0,|$\overrightarrow{a}$|=1=|$\overrightarrow{b}$|,求得k的值.
(2)由题意可得必存在λ,使$\overrightarrow{AB}$=λ•$\overrightarrow{BD}$,即2$\overrightarrow{a}$+k$\overrightarrow{b}$=λ(2$\overrightarrow{a}$-$\overrightarrow{b}$),由此求得k的值.
解答 解:(1)∵$\overrightarrow{AB}$⊥$\overrightarrow{BC}$,
∴$\overrightarrow{AB}•\overrightarrow{BC}$=(2$\overrightarrow{a}$+k$\overrightarrow{b}$)•($\overrightarrow{a}$+$\overrightarrow{b}$)=0,
再根据|$\overrightarrow{a}$|=1=|$\overrightarrow{b}$|,以及 $\overrightarrow{a}$•$\overrightarrow{b}$=0,
∴2${\overrightarrow{a}}^{2}$+k${\overrightarrow{b}}^{2}$=0,
∴2+k=0,
∴k=-2.
(2)由已A,B,D三点共线,可得必存在λ,使$\overrightarrow{AB}$=λ•$\overrightarrow{BD}$.
又 $\overrightarrow{BD}$=$\overrightarrow{BC}$+$\overrightarrow{CD}$=($\overrightarrow{a}$+$\overrightarrow{b}$)+($\overrightarrow{a}$-2$\overrightarrow{b}$)=2$\overrightarrow{a}$-$\overrightarrow{b}$,
∴$\overrightarrow{AB}$=2$\overrightarrow{a}$+k$\overrightarrow{b}$=λ(2$\overrightarrow{a}$-$\overrightarrow{b}$),
∴$\left\{\begin{array}{l}{2=2λ}\\{k=-λ}\end{array}\right.$,
求得k=-1,λ=1.
点评 本题主要考查两个向量的加减法及其几何意义,平面向量基本定理的应用,属于基础题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 原点对称 | B. | x轴对称 | C. | y轴对称 | D. | 直线y=x对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
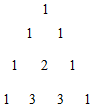 已知杨辉三角,将第4行的第一个数乘以1,第2个数乘以2,第3个数乘以4,第4个数乘以8后,这一行所以所有数字之和等于27(用数字作答):若等比数列{an}的前项是a1,公比是q(q≠1),将杨辉三角的第n+1行的第1个数乘以a1,第2个数乘以a2,…,第n+1个数乘以an+1后,这一行所有数字之和等于a1(1+q)n(用a1,q.n表示)
已知杨辉三角,将第4行的第一个数乘以1,第2个数乘以2,第3个数乘以4,第4个数乘以8后,这一行所以所有数字之和等于27(用数字作答):若等比数列{an}的前项是a1,公比是q(q≠1),将杨辉三角的第n+1行的第1个数乘以a1,第2个数乘以a2,…,第n+1个数乘以an+1后,这一行所有数字之和等于a1(1+q)n(用a1,q.n表示)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | (-∞,1) | C. | [2,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com