
【题目】现有甲、乙两个靶.某射手向甲靶射击一次,命中的概率为 ![]() ,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为
,命中得1分,没有命中得0分;向乙靶射击两次,每次命中的概率为 ![]() ,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击. (Ⅰ)求该射手恰好命中一次得的概率;
,每命中一次得2分,没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击. (Ⅰ)求该射手恰好命中一次得的概率;
(Ⅱ)求该射手的总得分X的分布列及数学期望EX.
【答案】解:(Ⅰ)记:“该射手恰好命中一次”为事件A,“该射手射击甲靶命中”为事件B,“该射手第一次射击乙靶命中”为事件C,“该射手第二次射击乙靶命中”为事件D 由题意知P(B)= ![]() ,P(C)=P(D)=
,P(C)=P(D)= ![]()
由于A=B ![]() +
+ ![]() +
+ ![]()
根据事件的独立性和互斥性得
P(A)=P(B ![]() )+P(
)+P( ![]() )+P(
)+P( ![]() )=P(B)P(
)=P(B)P( ![]() )P(
)P( ![]() )+P(
)+P( ![]() )P(C)P(
)P(C)P( ![]() )+P(
)+P( ![]() )P(
)P( ![]() )P(D)
)P(D)
= ![]() ×(1﹣
×(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )+(1﹣
)+(1﹣ ![]() )×
)× ![]() ×(1﹣
×(1﹣ ![]() )+(1﹣
)+(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )×
)× ![]()
= ![]()
(Ⅱ)根据题意,X的所有可能取值为0,1,2,3,4,5
根据事件的对立性和互斥性得
P(X=0)=P( ![]() )=(1﹣
)=(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )=
)= ![]()
P(X=1)=P(B ![]() )=
)= ![]() ×(1﹣
×(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )=
)= ![]()
P(X=2)=P( ![]() +
+ ![]() )=P(
)=P( ![]() )+P(
)+P( ![]() )=(1﹣
)=(1﹣ ![]() )×
)× ![]() ×(1﹣
×(1﹣ ![]() )+(1﹣
)+(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )×
)× ![]() =
= ![]()
P(X=3)=P(BC ![]() )+P(B
)+P(B ![]() D)=
D)= ![]() ×
× ![]() ×(1﹣
×(1﹣ ![]() )+
)+ ![]() ×(1﹣
×(1﹣ ![]() )×
)× ![]() =
= ![]()
P(X=4)=P( ![]() )=(1﹣
)=(1﹣ ![]() )×
)× ![]() ×
× ![]() =
= ![]()
P(X=5)=P(BCD)= ![]() ×
× ![]() ×
× ![]() =
= ![]()
故X的分布列为
X | 0 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
|
所以E(X)=0× ![]() +1×
+1× ![]() +2×
+2× ![]() +3×
+3× ![]() +4×
+4× ![]() +5×
+5× ![]() =
= ![]()
【解析】(Ⅰ)记:“该射手恰好命中一次”为事件A,“该射手射击甲靶命中”为事件B,“该射手第一次射击乙靶命中”为事件C,“该射手第二次射击乙靶命中”为事件D,由于A=B ![]() +
+ ![]() +
+ ![]() ,根据事件的独立性和互斥性可求出所求;(Ⅱ)根据题意,X的所有可能取值为0,1,2,3,4,根据事件的对立性和互斥性可得相应的概率,得到分布列,最后利用数学期望公式解之即可.
,根据事件的独立性和互斥性可求出所求;(Ⅱ)根据题意,X的所有可能取值为0,1,2,3,4,根据事件的对立性和互斥性可得相应的概率,得到分布列,最后利用数学期望公式解之即可.


科目:高中数学 来源: 题型:
【题目】数列{an}中,已知对任意n∈N* , a1+a2+a3+…+an=3n﹣1,则a12+a22+a32+…+an2等于( )
A.(3n﹣1)2
B.![]()
C.9n﹣1
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x-3)ex+ax,aR
(1)当a=1时,求曲线f(x)在点(2,f(2))处的切线方程;
(2)当a[0,e)时,设函数f(x)在(1,+)上的最小值为g(a),求函数g(a)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(sin
=(sin ![]() x,cos
x,cos ![]() x),
x), ![]() =(sin
=(sin ![]() x,
x, ![]() sin
sin ![]() x),x∈R,函数f(x)=
x),x∈R,函数f(x)= ![]() ,求:
,求:
(1)f(x)的最小正周期;
(2)f(x)在区间[0,1]上的最大值和最小值,以及取得最大值和最小值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是菱形,∠BAD=60°,侧面SAB⊥底面ABCD,并且SA=SB=AB=2,F为SD的中点. 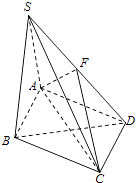
(1)求三棱锥S﹣FAC的体积;
(2)求直线BD与平面FAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
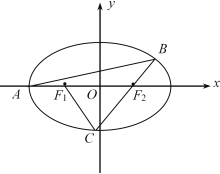
【题目】如图,已知椭圆![]() 的左顶点
的左顶点![]() ,且点
,且点![]() 在椭圆上,
在椭圆上, ![]() 、
、![]() 分别是椭圆的左、右焦点。过点
分别是椭圆的左、右焦点。过点![]() 作斜率为
作斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于点
于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为等腰三角形,求点
为等腰三角形,求点![]() 的坐标;
的坐标;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学校本课程开设了A,B,C,D共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生.
(1)求这3名学生选修课所有选法的总数;
(2)求恰有2门选修课没有被这3名学生选择的概率;
(3)求A选修课被这3名学生选择的人数ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国式过马路”是网友对部分中国人集体闯红灯现象的一种调侃,即“凑够一撮人就可以走了,和红绿灯无关.”出现这种现象是大家受法不责众的“从众”心理影响,从而不顾及交通安全.某校对全校学生过马路方式进行调查,在所有参与调查的人中,“跟从别人闯红灯”“从不闯红灯”“带头闯红灯”人数如表所示:
跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 | |
男生 | 800 | 450 | 200 |
女生 | 100 | 150 | 300 |
(1)在所有参与调查的人中,用分层抽样的方法抽取n人,已知“跟从别人闯红灯”的人中抽取45人,求n的值;
(2)在“带头闯红灯”的人中,将男生的200人编号为1,2,…,200;将女生的300人编号为201,202,…,500,用系统抽样的方法抽取4人参加“文明交通”宣传活动,若抽取的第一个人的编号为100,把抽取的4人看成一个总体,从这4人中任选取2人,求这两人均是女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣3x
(1)讨论f(x)的单调区间;
(2)若函数g(x)=f(x)﹣m在[﹣ ![]() ,3]上有三个零点,求实数m的取值范围;
,3]上有三个零点,求实数m的取值范围;
(3)设函数h(x)=ex﹣ex+4n2﹣2n(e为自然对数的底数),如果对任意的x1 , x2∈[ ![]() ,2],都有f(x1)≤h(x2)恒成立,求实数n的取值范围.
,2],都有f(x1)≤h(x2)恒成立,求实数n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com