
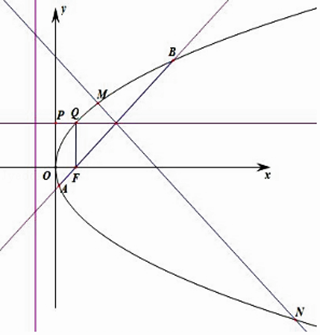
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,直线y=4与y轴的交点为P,与抛物线C的交点为Q,且|QF|=2|PQ|,过F的直线l与抛物线C相交于A,B两点.
(1)求C的方程;
(2)设AB的垂直平分线l'与C相交于M,N两点,试判断A,M,B,N四点是否在同一个圆上?若在,求出l的方程;若不在,说明理由.
【答案】
(1)解:设Q(x0,4),代入y2=2px得x0= ![]() ,
,
∴|PQ|= ![]() ,|QF|=
,|QF|= ![]() +x0=
+x0= ![]() +
+ ![]() .
.
由题设得 ![]() +
+ ![]() =2×
=2× ![]() ,解得p=﹣4(舍去)或p=4,
,解得p=﹣4(舍去)或p=4,
∴抛物线C的方程为y2=8x.
(2)解:由题设知,l与坐标轴不垂直,且过焦点F(2,0),
故可设l的方程为x=my+2(m≠0),
代入y2=8x得y2﹣8my﹣16=0.
设A(x1,y1),B(x2,y2),则y1+y2=8m,y1y2=﹣16.
故AB的中点为D(4m2+2,4m),
|AB|= ![]() |y1﹣y2|=
|y1﹣y2|= ![]()
![]() =8(m2+1).
=8(m2+1).
又l′⊥l,所以l′的斜率为﹣m,
所以l′的方程为x=﹣ ![]() y+4m2+6.
y+4m2+6.
将上式代入y2=8x,并整理得y2+ ![]() y﹣8(4m2+6)=0,
y﹣8(4m2+6)=0,
设M(x3,y3),N(x4,y4),
则y3+y4=﹣ ![]() ,y3y4=﹣8(4m2+6).
,y3y4=﹣8(4m2+6).
故MN的中点为E( ![]() +4m2+6,﹣
+4m2+6,﹣ ![]() ),
),
|MN|= ![]() |y3﹣y4|=
|y3﹣y4|= ![]()
![]() =
= ![]() ,
,
由于MN垂直平分AB,故A,M,B,N四点在同一圆上等价于|AE|=|BE|= ![]() |MN|,
|MN|,
又在Rt△ADE中,丨AD丨2+丨DE丨2=丨AE丨2,
从而 ![]() |AB|2+|DE|2=
|AB|2+|DE|2= ![]() |MN|2,
|MN|2,
即16(m2+1)2+(4m+ ![]() )2+(
)2+( ![]() +4)2=
+4)2= ![]() ,
,
化简得m2﹣1=0,m=±1,
所以当A,M,B,N四点在同一圆上时,l的方程为x=±y+2,即x±y﹣2=0.
【解析】(1)将Q(x0,4)代入抛物线方程,求得丨PQ丨,根据抛物线的定义,即可求得p的值,求得C的方程;(2)设l的方程为 x=my+1 (m≠0),代入抛物线方程化简,利用韦达定理、中点公式、弦长公式求得弦长|AB|.把直线l′的方程代入抛物线方程化简,利用韦达定理、弦长公式求得|MN|.由于MN垂直平分线段AB,故AMBN四点共圆等价于|AE|=|BE|= ![]() |MN|,由此求得m的值,可得直线l的方程.
|MN|,由此求得m的值,可得直线l的方程.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设f′(x)为函数f(x)的导函数,已知x2f′(x)+xf(x)=lnx,f(1)=![]() , 则下列结论正确的是( )
, 则下列结论正确的是( )
A.xf(x)在(0,+∞)单调递增
B.xf(x)在(1,+∞)单调递减
C.xf(x)在(0,+∞)上有极大值![]()
D.xf(x)在(0,+∞)上有极小值![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知D,E是△ABC边BC的三等分点,点P在线段DE上,若 ![]() =x
=x ![]() +y
+y ![]() ,则xy的取值范围是( )
,则xy的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分别为棱AA1 , AC的中点. 
(1)在平面ABC内过点A作AM∥平面PQB1交BC于点M,并写出作图步骤,但不要求证明;
(2)若侧面ACC1A1⊥侧面ABB1A1 , 求直线A1C1与平面PQB1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线 ![]() (t为参数)恒过椭圆
(t为参数)恒过椭圆 ![]() (φ为参数)在右焦点F.
(φ为参数)在右焦点F.
(1)求m的值;
(2)设直线l与椭圆C交于A,B两点,求|FA||FB|的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线  (t为参数),以原点为极点,以x正半轴为极轴,建立极坐标系,曲线
(t为参数),以原点为极点,以x正半轴为极轴,建立极坐标系,曲线 ![]() .
.
(Ⅰ)写出曲线C1的普通方程,曲线C2的直角坐标方程;
(Ⅱ)若M(1,0),且曲线C1与曲线C2交于两个不同的点A,B,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com